[Previous] [Contents] [Next]
[Comments or questions]

19 The Laws of Motion

There is no gravity.
The earth sucks.
— Physicist's bumper sticker

This chapter pulls together some basic physics ideas that are used in several places in the book.

We will pay special attention to rotary motion, since it is less familiar to most people than ordinary straight-line motion. Gyroscopes, in particular, behave very differently from ordinary non-spinning objects. It is amazing how strong the gyroscopic effects can be.

19.1 Straight-Line Motion

First, let's review the physical laws that govern straight-line motion. Although the main ideas go back to Galileo, we speak of Newton's laws, because he generalized the ideas and codified the laws.

The first law of motion states: ``A body at rest tends to remain at rest, while a body in motion tends to remain in motion in a straight line unless it is subjected to an outside force''. Although that may not sound like a very deep idea, it is one of the most revolutionary statements in the history of science. Before Galileo's time, people omitted frictional forces from their calculations. They considered friction ``natural'' and ubiquitous, not requiring explanation; if an object continued in steady motion, the force required to overcome friction was the only thing that required explanation. Galileo and Newton changed the viewpoint. Absence of friction is now considered the ``natural'' state, and frictional forces must be explained and accounted for just like any others.

The second law of motion says that if there is any change in the velocity of an object, the force required (F) is proportional to the mass (m) of the object, and proportional to the acceleration (a). (Acceleration is defined to be the rate-of-change of velocity.) In symbols,

F = m a (19.1)

The following restatement of the second law is often useful: since momentum is defined to be mass times velocity, and since the mass is not supposed to be changing, we conclude that the force is equal to the rate-of-change of the momentum. To put it the other way, change in momentum is force times time.

The third law of motion says that if a force is applied to an object, an equal and opposite force must be applied somewhere else. This, too, can be restated in terms of momentum: if we impart a certain momentum to an object, we must impart an equal and opposite amount of momentum to something else. ¹
This means that the total momentum of the world cannot change. This principle — conservation of momentum — is one of the most fundamental principles of physics, on a par with the conservation of energy discussed in chapter 1.

* Force is Not Motion

As simple as these laws are, they are widely misunderstood. For example, there is a widespread misconception that an airplane in a steady climb requires increased upward force and a steady descent requires reduced upward force. ²
Remember, lift is a force, and any unbalanced force would cause an acceleration, not steady flight.

In unaccelerated flight (including steady climbs and steady descents), the upward forces (mainly lift) must balance the downward forces (mainly gravity). If the airplane had an unbalanced upward force, it would not climb at a steady rate — it would accelerate upwards with an ever-increasing vertical speed.

Of course, during the transition from level flight to a steady climb an unbalanced vertical force must be applied momentarily, but the force is rather small. A climb rate of 500 fpm corresponds to a vertical velocity component of only 5 knots, so there is not much momentum in the vertical direction. The kinetic energy involved in the vertical motion is negligible.

In any case, once a steady climb is established, all the forces are in balance.

19.2 Sitting in a Rotating Frame

Suppose Moe is riding on a turntable; that is, a large, flat, smooth, horizontal rotating disk. Moe has painted an X, Y grid on the turntable, so he can easily measure positions, velocities, and accelerations relative to the rotating coordinate system. His friend Joe is nearby, observing Moe's adventures and measuring things relative to a nonrotating coordinate system.

Moe quickly notices that Newton's first law does not apply in a rotating reference frame. A hockey puck initially at rest on the floor (anywhere except right at the center of rotation) will be centrifuged outward.

In Joe's nonrotating frame, Newton's laws do apply. In a nonrotating frame, there is no such thing as centrifugal acceleration.

Moe holds the puck in place with a rubber band (one end attached to the puck, the other end attached to the floor).

Joe sees the same rubber band and the same force. The elongation of the rubber band indicates the magnitude of the force.

Moe says the puck is not moving relative to his reference frame. The rubber band compensates for the centrifugal force.

Joe says that the puck's momentum is constantly changing due to the rotation. The rubber band provides the necessary force.

19.3 Moving in a Rotating Frame

We now consider what happens to an object that is moving relative to a rotating reference frame.

Suppose Moe has another hockey puck, which he attaches by means of a rubber band to a tiny tractor. He drives the tractor in some arbitrary way. We watch as the puck passes various marks (A, B, etc.) on the floor.

Moe sees the puck move from mark A to mark B. The marks obviously are not moving relative to his reference frame.

Joe agrees that the puck moves from mark A to mark B, but he must account for the fact that the marks themselves are moving.

So let's see what happens when Joe analyzes the compound motion, including both the motion of the marks and the motion of the puck relative to the marks. He actually sees four contributions:

If the puck is accelerating relative to Moe's rotating frame, Joe agrees and counts that as a contribution to the acceleration. Both observers agree on how much force this requires.
From Joe's point of view, mark A is not only moving; its velocity is changing. Changing this component of the puck's velocity requires a force. (From Moe's point of view, this is the force needed to oppose centrifugal acceleration, as discussed previously.)
The velocity of mark B is different from the velocity of mark A. As the puck is towed along the path from point A to point B, the rubber band must provide a force in order to change the velocity so the puck can ``keep up with the Joneses''.
The velocity of the puck relative to the marks is also a velocity, and it must also rotate as the system rotates. This change in velocity also requires a force.

We can say a few words about each of these contributions from Moe's point of view:

This ``F=ma'' contribution is completely unsurprising. It is independent of position, independent of velocity, and independent of the frame's rotation rate.
The centrifugal contribution depends on position, but is independent of the velocity that Moe measures relative to his rotating reference frame. It is also independent of any acceleration created by Moe's tractor. It is proportional to the square of the frame's rotation rate.
This contribution is independent of position. It is proportional to the velocity that Moe measures, and is always perpendicular to that velocity. It is also proportional to the first power of the frame's rotation rate.
This contribution is also independent of position. It is also proportional to the velocity relative to the rotating frame, and is perpendicular to that velocity, and is proportional to the first power of the frame's rotation rate.

Contribution #3 is numerically equal to contribution #4. The total effect is just twice what you would get from either contribution separately. Together these two contributions are called the Coriolis effect.³

The Coriolis effect can be described as an acceleration (proportional to the object's velocity), and equivalently it can be described as a force (proportional to the object's momentum).

Let's consider a reference frame attached to an eastward-rotating rotating planet, such as the earth. Near the north pole, the Coriolis acceleration is always toward your right, if you are facing forward along the direction of motion. Northward motion produces a Coriolis acceleration to the east; a very real westward force is necessary to oppose it if you want to follow a straight line painted on the earth. Eastward motion produces a Coriolis acceleration to the south; a very real northward force is necessary to oppose it.

The Coriolis argument only applies to motion in the plane of rotation. Momentum parallel to the axis is unaffected. In all cases the Coriolis acceleration lies in the plane of rotation and perpendicular to the motion.

Near the equator, we have to be careful, because the plane of rotation is not horizontal. In this region, eastward motion produces a Coriolis acceleration in the upward direction, while westward motion produces a Coriolis acceleration in the downward direction. In this region, north/south motions are parallel to the axis of rotation and produce no Coriolis effects.

To reiterate: The Coriolis effect and the centrifugal field are two separate contributions to the story. The Coriolis effect applies only to objects that are moving relative to the rotating reference frame. The centrifugal field affects all objects in the rotating frame, whether they are moving or not.

* Magnitude of the Effect

Suppose you are in an airplane, flying straight ahead at 120 knots along the shortest path between two points on the earth's surface. Because of the rotation of the earth, the airplane will be subject to a Coriolis acceleration of about 0.001G. This is too small to be noticeable.

Now suppose you and a friend are standing 60 feet apart, playing catch in the back of a cargo plane while it is performing a standard-rate turn (three degrees per second). If your friend throws you the ball at 60 mph, it will be subject to a horizontal Coriolis acceleration of more than a quarter G. That means the ball will be deflected sideways about 2 ½ feet before it gets to you — which is enough to be quite noticeable. In normal flying, though, we don't often throw things far enough to produce large Coriolis effects.

The wind, moving relative to the rotating earth, is subject to a Coriolis acceleration that is small but steady; the cumulative effect is tremendously important, as discussed in section 20.1.

19.4 Centrifuges with and without Gravity

19.4.1 The Centrifugal Field is Real

An airplane in a turn, especially a steep turn, behaves like a centrifuge. There are profound analogies between centrifugal and gravitational fields:

The gravitational field at any given point is an acceleration. It acts on objects, producing a force in proportion to the object's mass.

The centrifugal field at any given point is also an acceleration. It, too, acts on objects, producing a force in proportion to the object's mass.

Strictly speaking, neither gravity nor centrifugity is a ``force'' field. Each is really an acceleration field. Of course there is a force involved, but it is always a force per unit mass, which is properly called an acceleration.

Einstein's principle of equivalence states that at any given point, the gravitational field is indistinguishable from an acceleration of the reference frame.⁴ In a freely-falling reference frame, such as a freely-orbiting space station, everything is weightless.

My laboratory is not a free-falling inertial frame. It is being shoved skyward as the earth pushes on its foundations. If you measure things relative to the laboratory walls, you will observe gravitational accelerations.

Similarly, the cabin of a centrifuge is clearly not an inertial frame. If you measure things relative to the cabin, you will observe centrifugal accelerations.

From a modern-physics point of view, both gravity and centrifugity emerge as consequences of working in an accelerated frame. There is nothing wrong with doing so, provided the work is done carefully. Accounting for centrifugal effects is not much trickier than accounting for gravitational effects. When people think this can't be done, it is just because they don't know how to do it.

For a ground-bound observer analyzing the flight of an airplane, it may be convenient to use a reference frame where gravity exists and centrifugity does not. However, the pilot and passengers usually find it convenient to use a frame that includes both gravity and centrifugity.

The centrifugal field is not crude or informal or magical. (The problem with magic is that it can explain false things just as easily as true things.) Like the gravitational field, it is a precise way of accounting for what happens when you work in a non-freely-falling reference frame.

19.4.2 Centrifuge

To get a better understanding of the balance of forces in a turning and/or slipping airplane, consider the centrifuge shown in figure 19.1. For the moment we will neglect the effects of gravity; imagine this centrifuge is operating in the weightless environment of a space station. We are riding inside the centrifuge cabin, which is shown in red. We have a supply of green tennis balls. At point A (the southernmost point of our path) we drop a tennis ball, whereupon it flies off as a free particle. Our centrifuge continues to follow its circular path.

Figure 19.1: An Object Departing a Centrifuge

Case 1a: Consider the point of view of a bystander (not riding in the centrifuge). The dropped tennis ball moves in a straight line, according to the first law of motion. Contrary to a common misconception, the bystander does not see the ball fly radially away from the center of the centrifuge. It just continues with the purely eastward velocity it had at point A, moving tangentially.

Case 1b: Consider our point of view as we ride in the centrifuge. At point A, the tennis ball has no velocity relative to us. For the first instant, it moves along with us, but then gradually it starts moving away. We do see the ball accelerate away in the purely radial direction. The tennis ball — like everything else in or near the centrifuge — seems to be subjected to a centrifugal acceleration field.

Einstein's principle of equivalence guarantees that our viewpoint and the bystander's viewpoint are equally valid. The bystander says that the centrifuge cabin and its occupants accelerate away from the freely moving tennis ball, while we say that the tennis ball accelerates away from us under the influence of the centrifugal field.

There is one pitfall that must be avoided: you can't freely mix the two viewpoints. It would be a complete fallacy for the bystander to say ``gee, the folks in the cabin told me the tennis ball accelerated outward; therefore it must move to the south starting from point A''. In fact, the free-flying ball does not accelerate relative to the bystander. It will not wind up even one millimeter south of point A. It will indeed wind up south of our centrifuge cabin, but only because we have peeled off to the north.

Case 2a: Consider from the bystander's point of view what happens to a ball that has not been released, but is just sitting on a seat in the centrifuge. The bystander sees the ball subjected to an unbalanced force, causing it to move in a non-straight path relative to the earth.

Case 2b: Consider the seated ball from the centrifuge-riders' point of view. The force on the ball exerted by the seat is just enough to cancel the force due to centrifugal acceleration, so the forces are in balance and the ball does not move.

When analyzing unsteady motion, or when trying to calculate the motion of the centrifuge itself, it is often simpler to analyze everything from the bystander's point of view, in which the centrifugal field will not appear. On the other hand, in a steady turn, is often easy and natural to use the centrifuge-riders' point of view; in which all objects will be subject to centrifugal accelerations.

19.4.3 Centrifuge and Gravity

Now that we understand the basic idea, let's see what happens when our centrifuge operates in the normal gravitational field of the earth. This is shown in figure 19.2. When the tennis ball departs the centrifuge, it once again travels in a purely easterly direction, but this time it also accelerates downward under the influence of gravity.

Figure 19.2: An Object Departing a Centrifuge, with Gravity

Once again, from inside the cabin we observe that the tennis ball initially accelerates away in the direction exactly away from the pivot of the centrifuge. This is no coincidence; it is because the only difference between our motion and the free-particle motion comes from the force in the cable that attaches us to the pivot.

(The foregoing applies only to the initial acceleration of the dropped ball. As soon as it picks up an appreciable velocity relative to us, we need to account for Coriolis acceleration as well as centrifugal acceleration.)

Remember, the equivalence principle says that at each point in space, a gravitational field is indistinguishable from an accelerated reference frame. Therefore we need not know or care whether the tennis ball moves away from us because we are being accelerated, or because there is a gravitating planet in the vicinity, or both.

19.5 Centrifugal Effects in a Turning Airplane

Let's examine the forces felt by the pilot in a turning airplane. We start with a coordinated turn, as shown in figure 19.3.

Figure 19.3: Airplane in a Coordinated Turn

In figures such as this, whenever I am analysing things using the pilot's point of view, the figure will include a rectanglular ``frame'' with a little stick figure (the observer) standing in the corner. It is important to carefully specify what frame is being used, because even simple questions like ``which way is down'' have answers that depend on which observer you ask. In particular, I define N-down (Newtonian down) to mean the direction straight down toward the center of the earth. In contrast, I define E-down (effective down, or Einsteinian down) to be the direction in which a free particle departs if you drop it. In a turning airplane, the two directions are not the same.

Using your inner ear, the seat of your pants, and/or the inclinometer ball, you can tell which way is E-down. Using the natural horizon and/or the artificial horizon, you can tell which way is N-down.

In figure 19.3, assume the airplane's mass is one ton. Real gravity exerts a force of one ton, straight down toward the center of the earth. The airplane is an a 45^° bank, so there is one ton of centrifugal force, sideways, parallel to the earth's horizon. All in all, the wings are producing 1.41 tons of lift, angled as shown in the figure.

Figure 19.4: Inclinometer in a Coordinated Turn

Figure 19.4 shows the same situation, and analyzes the forces on the inclinometer ball. Real gravity exerts a downward force on the ball, and centrifugity exerts a sideways force. The tubular race that contains the ball exerts a force perpendicular to the wall of the race (whereas the ball is free to roll in the direction along the race). The race-force balances the other forces when the ball is in the middle, confirming that this is a coordinated turn.

As a contrast, consider figure 19.5, which shows what happens if you make a boat turn. (Boat turns are discussed in section 8.10.)

Because the airplane is turning, it and everything in it will be subjected to a centrifugal acceleration (according to the viewpoint of the centrifuge riders).

Figure 19.5: Airplane in a Boat Turn

Figure 19.6 shows how the inclinometer ball responds to a boat turn. Gravity still exerts a force on the ball, straight down. Centrifugity exerts a force sideways toward the outside of the turn. The ball is subject to a force of constraint, perpendicular to the walls of the race. (It is free to roll in the other direction.) The only place in the race where this constraint is in a direction to balance the other forces is shown in the figure. The ball has been ``centrifuged'' toward the outside of the turn. This is a quantitative indication that the E-down direction is not perpendicular to the wings, and some force other than wing-lift is acting on the plane.

Figure 19.6: Inclinometer in a Boat Turn

Figure 19.7: Airplane in a Nonturning Slip

Figure 19.8: Inclinometer in a Nonturning Slip

Finally, figure 19.7 shows the forces on the airplane in an ordinary nonturning slip. The right rudder pedal is depressed, and the port wing has been lowered just enough that the horizontal component of lift cancels the horizontal force due to the crossflow over the fuselage. The airplane is not turning. The bystander and the riders agree that there is no centrifugal field. Figure 19.8 shows the forces on the inclinometer ball in the same situation.

19.6 Angles and Axes

19.6.1 Axes: Yaw, Pitch, and Roll

The standard definitions of the yaw, pitch, and roll axes are shown in figure 19.9.

Figure 19.9: Yaw, Pitch, and Roll Axes

Many older books refer to the pitch axis as the lateral axis and the roll axis as the longitudinal axis, which are sensible enough, but then they refer to pitch-axis stability as longitudinal stability and roll-axis stability as lateral stability — which seems completely reversed and is confusing at best. Reference 22 calls the yaw axis the normal axis, since it is normal (i.e. perpendicular) to the other axes — but that isn't very helpful since all the axes are normal to all the others. Other references call the yaw axis the vertical axis, but that is very confusing since if the bank attitude or pitch attitude is not level, the yaw axis will not be vertical.

Obviously the new terminology is an improvement. The situation is summarized in the following table.

This Book

Older Terminology

pitch axis

lateral axis

pitch-axis stability

longitudinal stability

roll axis

longitudinal axis

roll-axis stability

lateral stability

yaw axis

vertical axis

yaw-axis stability

directional stability

19.6.2 Attitude: Heading, Pitch, Bank

The term attitude describes the orientation of the airplane's axes relative to the earth. Attitude is specified in terms of three angles: the heading, the pitch attitude, and the bank attitude.

To place the airplane in a specified attitude, start with the airplane in level flight (i.e. X axis and Y axis horizontal) and with the airplane pointed north. Then

Rotate the airplane around the yaw axis by the specified heading angle. A positive angle specifies a clockwise rotation as seen from above, so that a heading of 090 degrees corresponds to pointing east and a heading of 180 degrees corresponds to pointing south.
Rotate the airplane around the pitch axis by the specified pitch attitude angle. A positive angle specifies a nose-up attitude.
Rotate the airplane around the roll axis by the specified bank attitude angle. A positive angle corresponds to clockwise as seen from the rear.

As discussed below (section 19.6.4), it is important to perform these rotations in the order specified.

We have just seen how, given a set of angles, we can put the airplane into a specified attitude. We now consider the reverse question: given an airplane in some attitude, how do we determine the angles that describe that attitude?

Answer: just figure out what it would take to return the airplane to level northbound flight. The rotations must be undone in the reverse of the standard order:

First, rotate the aircraft around the roll axis until the wings are level. This determines the bank attitude.
Second, rotate the aircraft around the pitch axis until the X axis is level. This determines the pitch attitude. Note that this rotation is not performed around the original pitch axis, but rather around the new pitch axis, which is horizontal as a consequence of the previous step.
Finally, rotate the aircraft around the (new) yaw axis until the nose is pointing north. This determines the heading.

19.6.3 Angle Terminology

The following table summarizes the various nouns and verbs that apply to angles and motions around the three axes.

	Z axis	Y axis	X axis
Motion	it yaws	it pitches	it rolls
Angle	the heading	the pitch attitude	the bank attitude

There are a few more fine points of X-axis terminology:

Saying that the airplane is ``banking'' or ``in a bank'' refers to a definite bank attitude.
In contrast, saying that the airplane is ``rolling'' or ``in a roll'' refers to a definite rate of rotation, i.e. a changing bank angle.
Pitch angle usually means the same thing as pitch attitude.
Bank angle usually means the same thing as bank attitude.
The term roll angle is a rarely-used synonym for bank angle.

* Other Angles

To define the angle of attack of the fuselage, take the direction of flight (or its reciprocal, the relative wind) and project it onto the XZ plane. The angle of attack is the angle between this projection and the X axis or some other convenient reference.

To define the slip angle, take the direction of flight (or the relative wind) and project it onto the XY plane. The slip angle is the angle between this projection and the X axis.

Some aerodynamics texts use the term sideslip angle, which is synonymous with slip angle. This may be confusing because some pilot-training books try to draw a distinction between a forward slip and a side slip, even though the difference is imaginary, as is discussed in conjunction with figure 11.1.

19.6.4 Yaw Does Not Commute with Pitch

It is a fundamental fact of geometry that the result of a sequence of rotations depends on the order in which the rotations are performed.

Note that for a sequence of ordinary non-rotational movements, the ordering does not matter. That is, suppose I have two small objects that start out at the same place. I move one object move two feet north, and then three feet west. I move the other object the same distances in the other order: three feet west and then two feet north. Assuming there are no obstructions, both objects will arrive at the same destination. The ordering of the movements does not matter.

However, angles don't play by the same rules as distances. For instance, it is possible to change the yaw angle (i.e., the heading) by 37 degrees (or any other amount) without ever yawing the plane. That is:

You can pull up into aerobatic vertical flight, use the ailerons to rotate 37 degrees around the now-vertical roll axis, and then push back to level flight.
Another way to do the same thing is to roll into a ninety-degree bank, pull on the yoke to rotate around the now-vertical pitch axis by 37 degrees, and then roll back to wings-level attitude.

If the aircraft (and its occupants) can tolerate heavy G loads, such maneuvers are perfectly fine ways to make tight turns at high airspeed.

In non-aerobatic flight, a less-extreme statement applies: a rotation in a purely horizontal plane is not a pure yaw when the aircraft is not in a level attitude. For instance, suppose you are in level flight, steadily turning to the left. This is, of course, a turn around an axis that runs vertically through the center of the earth. Further suppose that you have a nose-up pitch attitude, while still maintaining a level flight path. This means that the airplane's yaw axis (Z axis) is not vertical. You could, in principle, perform the required heading change by pitching down to level pitch attitude, performing a pure yaw, and then pitching back up, but since rotations are not commutative this is not equivalent to maintaining your pitch attitude and performing a pure yaw. Performing the required change of heading without pitching down requires mostly pure leftward yaw, but involves some rightward rotation around the airplane's roll axis as well.

The analysis in the previous paragraph is 100% accurate, but completely irrelevant when you are piloting the airplane. ⁵ In particular, the rotation around the roll axis does not raise the angle of attack on one wingtip or lower it on the other. Arguing about whether the heading change is a pure yaw or a yaw plus roll is almost like arguing about whether a glass of water is half full or half empty — the physics is the same. In this case the physics is simple: the inside (left) wing follows a horizontal circular path, while the outside (right) wing follows a slightly longer horizontal path around a larger circle.

It is easy to see why that is so: The turn requires a rotation around a vertical axis. Such a rotation moves the wingtips (and everything else) in purely horizontal directions. As long as the airplane's center-of-mass motion is also horizontal, the rotation can only change the speeds, not the angles, of the airflow.

Now, things get more interesting when the direction of flight is not horizontal. Therefore let us consider a new example in which you are climbing while turning. That means your flight path is inclined above the horizontal. As before, you are turning to the left at a steady rate.

In any halfway-reasonable situation, the yaw axis will be nearly perpendicular to the direction of flight. Having it not exactly perpendicular is just a distraction from the present topic, so I hereby define a new ``yaw-like'' axis exactly perpendicular the direction of flight. It is also perpendicular to the pitch axis (which remains parallel to the wingtip-to-wingtip direction). The third axis is a new ``roll-like'' axis perpendicular to the other two. If we assume zero slip angle, it will be aligned with the direction of flight.

As the airplane flies from point to point along its curving path, its heading must change. This is a rotatation around a purely vertical axis. In climbing flight, the yaw-like axis is not vertical, so the turn is not pure yaw. The turn moves the inside wingtip horizontally backwards, relative to where it would be if there were no heading change. In contrast, a pure yaw-like rotation would have moved the wing back and down. Therefore we need not just leftward yaw-like rotation but also some rightward roll-like rotation to keep the wingtip moving along the actual flight path.

This roll-like motion means that (other things being equal) the inside wingtip would fly at a lower angle of attack during a climbing turn. Less lift would be produced. You need to deflect the ailerons to the outside to compensate.

Note that I said less lift ``would be'' produced, not ``is'' produced. Because you have compensated with the ailerons, both wings are in fact producing the same amount of lift, as they should. Remember that this is a steady turn, so no force is required to maintain the steady roll rate. (Remember, according to Newton's laws, an unbalanced force would create an acceleration around the roll axis, which is not what is happening here.) There are widespread misconceptions about this. Because of the roll-like motion, the air will arrive at the two wings from two different directions. You will have to deflect the ailerons, not in order to create a magnitude of lift, but rather to keep from creating a different magnitude of lift.

Although the magnitude of the lift remains the same, the direction of the lift will be twisted, as discussed in section 8.8.4; see in particular figure 8.7. You will need to deflect the rudder to overcome the resulting yawing moment. This will be in the usual direction: right rudder in proportion to right aileron deflection, and left rudder in proportion to left aileron deflection.

In a climbing turn, the differential relative wind combines with the differential wingtip velocity to create a large overbanking tendency. In an ordinary descending turn, the relative wind effect tends to oppose the velocity effect. In a spin, the differential relative wind is a key ingredient, as discussed in section 18.6.1, including figure 18.6. Also, section 9.7 analyzes climbing and descending turns in slightly different words and gives a numerical example.

19.6.5 Yaw Does Not Commute with Bank

As stated above, a rotation in a purely horizontal plane is not a pure yaw when the aircraft is not in a level attitude. In the previous section we considered the consequences of a non-level pitch attitude, but the same logic applies to a non-level bank attitude. The latter case is in some sense more significant, since although not all turns involve a non-level pitch attitude, they almost always involve a bank.

You could perform the required rotation by rolling to a level attitude, performing a pure yaw, and then rolling back to the banked attitude. This is not equivalent to performing a pure yaw while maintaining constant bank. For modest bank angles, the constant-bank maneuver is mostly pure yaw, but involves some rotation around the pitch axis as well. Because of this rotation around the pitch axis, the relative wind hits the wing and the tail at slightly different angles. You will need to pull back on the yoke slightly to compensate. This pull is in addition to whatever pull you might use for controlling airspeed during the turn. You can see that the two phenomena are definitely distinct, by the following argument: suppose that you maintain constant angle of attack during the turn, so that the required load factor is produced by increased airspeed not increased angle of attack. You would still need to pull back a little bit, to overcome the noncommutativity.

19.7 Torque and Moment

Just as Newton's first law says that to start an object moving you have to apply a force, there is a corresponding law that says to start an object turning you need to apply a torque.

You may have heard of the word ``torque'' in conjunction with left-turning tendency on takeoff, and you may have heard of the word ``moment'' in conjunction with weight & balance problems. In a deep sense, the two words are two names for the same thing. In particular,

A rolling moment is a torque around the roll axis.
A pitching moment is a torque around the pitch axis.
A yawing moment is a torque around the yaw axis.

A familiar example: fuel and cargo cause a pitching moment, depending on how far forward or aft they are loaded. By the same token, they will cause a rolling moment if they are loaded asymmetrically left or right.

Another familiar example: gyroscopic effects can cause torque around the yaw axis. By the same token, they can cause torque around the pitch axis as well.

I will use the terms ``torque'' and ``moment'' interchangeably.

Torque is not the same as force. Of the two, force is the more familiar concept. If you attach a string to an object and pull, the object is subjected to a force in the direction of the string. Force is measured in pounds or newtons.

To apply a torque, you need a force and a lever-arm. The amount of torque is given by the following formula:

torque = force × distance (19.2)

where the distance is a vector representing the separation between the pivot-point⁶ and the point where the force is applied. In this formula, we are using the vector cross product,⁷ indicating that we only count the component of the distance perpendicular to the force. This quantity (the component of the distance perpendicular to the force) is called the lever arm, which makes it convenient to say that the torque is the force times the lever arm.

Torque is measured not in pounds but in footpounds (that is, feet times pounds); the corresponding metric unit is newtonmeters. ⁸
Figure 19.10 shows a situation where all the forces and torques are in balance. On the right side of the bar, a group of three springs is exerting a force of 30 pounds. On the left side of the bar, there is a group of two springs (exerting a force of 20 pounds) and a single spring (exerting a force of 10 pounds). Since the total leftward force equals the total rightward force, the forces are in balance.

Figure 19.10: Forces and Torques in Balance

To show that the torques are in balance requires a separate check. Let's choose the point marked ``x'' as our pivot point. The rightward force produces no torque, because it is attached right at the pivot point — it has a zero-length lever arm. The group of two springs produces a counterclockwise torque, and the single spring produces a clockwise torque of the same magnitude, because even though it has half as much force it has twice the lever arm. The torques cancel. The system is in equilibrium.

Figure 19.11: Forces in Balance but Torques NOT in Balance

Figure 19.11 shows a different situation. The forces are in balance (20 pounds to the right, 20 pounds total to the left) but the torques are not in balance. One of the left-pulling springs has twice the lever arm, producing a net clockwise torque. If you tried to set up a system like this, the bar would immediately start turning clockwise. The system is out of equilibrium.

Torque is a vector; that is, it has direction as well as magnitude. A torque around a given axis is represented by a torque vector along that axis. In particular, the clockwise torque in figure 19.11 is represented by a vector perpendicular to the paper, directed away from the reader.

19.8 Angular Momentum

The notion of angular momentum is the key to really understanding rotating objects.

Angular momentum is related to ordinary straight-line momentum in the same way that torque is related to ordinary straight-line force. Here is a summary of the correspondences:

Straight-line concept

Angular concept

Force

Torque (equals force times lever arm)

Momentum

Angular momentum (equals ordinary momentum times lever arm)

The ordinary momentum of a system won't change unless a force is applied.

The angular momentum of a system won't change unless a torque is applied.

The change in straight-line momentum is the force times the time.

The change in angular momentum is the torque times the time.

When I give lectures, I illustrate conservation of angular momentum using a demo you can easily set up for yourself. As illustrated in figure 19.12, tie some kite string to a small bean-bag and swing it in a circle. When you pull on the free end of the string (reducing the radius of the circle) the bean-bag speeds up. When you let out the string (increasing the radius of the circle) the bean-bag slows down.⁹

Figure 19.12: Conservation of Angular Momentum

In typical textbooks, conservation of angular momentum is exemplified by spinning ice skaters, but I find it easier to travel with a bean-bag (rather than an ice skater) in my luggage.

In the demonstration, there are some minor torques due to friction than will eventually slow down the bean-bag whether or not you shorten or lengthen the string, but if you perform the experiment quickly enough the torques can be neglected, and the angular momentum of the system is more or less constant. Therefore, if you decrease the lever arm by a factor of N, the straight-line momentum must increase by a factor of N (since their product cannot change).¹⁰

Since the tangential velocity increases by a factor of N, and the radius decreases by a factor of N, the rate of turn (degrees per second) increases by a factor of N squared.

The energy of the system also increases by a factor of N squared. You can feel that you added energy to the system when you pull on the string, pulling against tension.

So far we have analyzed the situation from the point of view of a bystander in a non-rotating reference frame. You can reach the same conclusion by analyzing the situation in the rotating reference frame, as would apply to an ant riding on the bean-bag. The ant would say that as the string is pulled in, the bean-bag accelerates sideways because of the Coriolis effect, as discussed in section 19.3.

Conservation of angular momentum applies to airplanes as well as bean-bags. For instance, consider an airplane in a flat spin, as discussed in section 18.6.4. In order to recover from the spin, you need to push the nose down. This means whatever mass is in the nose and tail will move closer to the axis of rotation. The angular momentum of the airplane doesn't change (in the short run), so the rotation will speed up (in the short run). More rotation may seem like the opposite of what you wanted, but remember you are trying to get rid of angular momentum, not just angular rate. You should persevere and force the nose down. Then the aerodynamic forces (or, rather, torques) will carry angular momentum out of the system and the rotation will decrease.

Angular momentum is a vector; that is, it has direction as well as magnitude. The angular momentum vector points more-or-less¹¹ along the axis of rotation. In particular, the angular momentum of an aircraft propeller (rotating clockwise as viewed from behind) is directed forward along the axis of rotation.

19.9 Gyroscopes

19.9.1 Precession

For any normal object (such as a book) if you apply a force in a given direction, it will respond with motion in that direction. People are so accustomed to this behavior that they lose sight of the fact that force and motion are not exactly the same thing, and they don't always go together.

In particular, for a gyroscope, if you apply a torque around one axis, it will respond with motion around a different axis. When I give my ``See How It Flies'' lectures, I carry around a bicycle wheel with handles, as shown in figure 19.13. The indicated direction of spin corresponds to a normal American engine and propeller, if the nose of the airplane is toward the left side of the diagram.

Figure 19.13: Bicycle Wheel with Handles

To demonstrate the remarkable behavior of a gyroscope, I stand behind the ``propeller'' (on the right side of the diagram) and support its weight by lifting the rear handle only. The force of gravity acts on the center of the system, so there is a pure nose-down / tail-up pitching moment. If this were a normal, non-spinning object, it would respond by pitching in the obvious way, but the gyroscope actually responds with a pure yawing motion. I have to turn around and around to my left to stay behind the wheel.

It is really quite amazing that the wheel does not pitch down. Even though I am applying a pitching force, the wheel doesn't pitch down; it just yaws around and around.

Figure 19.14: Gyroscopic Precession

This phenomenon, where a gyro responds to a torque about one axis with a motion about another axis, is called gyroscopic precession.

Precession is often quite noticeable at the point where a taildragger raises the tail, early in the takeoff roll. If the airplane were an ordinary non-spinning object, you could raise the tail using the flippers alone. But note that airflow over the flippers does not actually dictate the motion of the airplane; it just produces a force and a torque around the pitch axis. For a gyroscope, a torque around the pitch axis produces a motion around the yaw axis. If you try to raise the tail of a real airplane using flippers alone, it will yaw to the left because of precession.

To get a gyroscope to actually move around the pitch axis, you need to apply a torque around the yaw axis — using the rudder.

Of course, an airplane has some plain old mass in addition to its gyroscopic properties. In order to lift this ordinary mass you need to use the flippers. Therefore, the tail-raising maneuver requires both flippers and rudder — flippers to change the pitch of the ordinary mass, and rudder to change the pitch of the gyroscope.

19.9.2 The Torque is 90 Degrees Ahead of the Motion

Now that you've got the idea that a torque around the pitch axis causes a motion around the yaw axis, you may be wondering how to figure out the direction. Will it be yaw to the right, or yaw to the left? There is a simple rule: the axis of the applied torque will be 90 degrees ahead of the axis of the motion.¹² An application of this rule is depicted in figure 19.15.

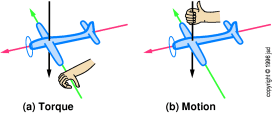Figure 19.15: The Applied Torque is 90 Degrees Ahead of The Motion

If you apply forward pressure on the yoke, it applies a torque around the pitch axis in the direction that your fingers curl in figure 19.15(a).¹³

Now rotate your hand 90 degrees in the direction that the propeller is spinning. Your fingers now specify the direction of motion, as shown in figure 19.15(b). The nose will move to the left.

Conclusion: forward pressure on the yoke makes the nose move to the left.

As another application of this rule, you can convince yourself that right rudder deflection will cause a nose-down / tail-up pitching motion.

The applied torque is 90 degrees ahead of the motion.

Superficially, this gyroscope law is reminiscent of the Coriolis effect (force in one direction, motion in a perpendicular direction) but they do not represent the same physics. The Coriolis law only applies to objects that are moving relative to a rotating observer. In contrast, the gyroscope law applies to a stationary observer; no parts of the gyroscope are moving relative to each other.

19.9.3 Angular Momentum is the Key Idea

Precession, and all the other gyro effects discussed in this section, are direct consequences of the angular momentum laws discussed in the previous section.

Figure 19.16: Angular Momentum Explains Precession

Figure 19.16 is the same as figure 19.14, but with the torque and angular momentum vectors drawn in. The torque around the pitch axis is represented by a vector along the pitch axis — to my left if I am standing behind the wheel. The angular momentum is represented by a vector along the axis of rotation, directed away from me since the wheel is spinning clockwise as seen from behind. The change in angular momentum is (according to the laws of motion) equal to the torque times the time.

The figure shows what happens during one unit of time (one second). The new angular momentum is the vector sum of the old angular momentum, plus the torque times the time. Since we are considering one second, the change vector is equal in magnitude to the torque vector.

During subsequent seconds, the torque vector will be a new direction because the whole system has rotated. The successive changes will pull the angular momentum vector around in a horizontal circle.

Gyroscopic effects only occur when the orientation of the gyro axis is changing. You can take a gyro and transport it north/south, east/west, or up/down, without causing any precession, as long as the gyro axis remains pointed in the same direction. You can even roll an airplane without seeing gyroscopic effects, since the roll leaves the gyro axis pointing in the same direction.

If you have a lightweight airframe and a heavy, rapidly spinning propeller, watch out: the flippers will cause yawing motion and the rudder will cause pitching motion.

If you want to make a gyro change orientation quickly, it will take more torque than doing it slowly.

19.9.4 Inertial Platform

We now consider what happens when a gyro is not subjected to any large torques.

Suppose we support a gyroscope on gimbals. The gimbals support its weight but do not transmit any torques to it, even if the airplane to which the gimbals are mounted is turning. We call this a free gyro since it is free to not turn when the airplane turns.

Even though the gyro is small, it has a huge amount of angular momentum, because it is spinning so rapidly. Any small torque applied to the gyro (because of inevitable imperfections in the gimbals) will, over time, change the angular momentum — but over reasonably short times the change is negligible compared to the total.

In such a situation, the gyro will tend to maintain fixed orientation in space. We say that the gyro is an inertial platform with respect to rotations.¹⁴ Other books say the gyro exhibits rigidity in space but that expression seems a bit odd to me.

19.10 Gyroscopic Instruments

We now discuss the principles of operation of the three main gyroscopic instruments: artificial horizon gyro (attitude indicator), the directional gyro (heading indicator), and the rate of turn gyro (turn needle or turn coordinator).

19.10.1 Heading Indicator

The directional gyro is a free gyro. It establishes an inertial platform.

The gyro spins in some vertical plane; that is, its angular momentum vector points in some arbitrary horizontal direction. A system of gears measures the angle that the angular momentum vector makes in the XY plane¹⁵ and displays it to the pilot. The trick is to measure the angle and support the gyro while minimizing the accidental torques on it. Imperfections in the mechanism cause the gyro to precess; therefore, every so often the heading indication must be corrected, typically by reference to a magnetic compass.

19.10.2 Artificial Horizon

The artificial horizon (also known as the attitude indicator) is another free gyro. This gyro's plane of rotation is horizontal; that is, its angular momentum vector is vertical. A mechanical linkage measures the angle that this vector makes in the YZ (bank) and XZ (pitch) planes, and displays it to the pilot.

It is instructive to compare the horizon gyro (which tells you which way is ``down'') with the inclinometer ball or a plumb-bob on a string (which has a different notion of which way is ``down''). The distinction is that the plumb-bob tells you which way is E-down, while the gyro is designed to tell you which way is N-down (toward the center of the earth). Whenever the airplane is being accelerated (e.g. during the takeoff roll or during a turn), the two directions are quite different. As seen in figure 19.17, during a turn the E-down vector gets centrifuged to the outside of the turn; the N-down vector always points to the center of the earth.

Figure 19.17: E-Down versus N-down During a Turn

To a first approximation, the horizon gyro works just by remembering which way is N-down. However, no gyro can remember anything forever, so the instrument contains an ``erecting mechanism'' that makes continual small adjustments. You would like it to align the gyro axis with N-down — but the mechanism doesn't know which way is N-down! It knows which way is E-down (the same way the plumb-bob does), but according to Einstein's principle of equivalence , it cannot possibly know what components of E-down are due to gravity and what components are due to acceleration. The erecting mechanism does, in fact, continually nudge the gyro axis toward E-down, but the result is a good approximation to N-down, for the following reason: if you average the E-down vectors over an entire turn, they average out to N-down. As you can see in the figure:

sometimes E-down points a little to the north of N-down,
sometimes E-down points a little to the west of N-down,
sometimes E-down points a little to the south of N-down,
sometimes E-down points a little to the east of N-down.

If you average the discrepancies over an entire turn, they cancel.

* Artificial Horizon Errors

Of course, if you only make half a turn, the discrepancies don't average to zero, and the attitude indicator will be slightly inaccurate for a while. Analogous errors occur during takeoff, because the gyro's estimate of ``down'' gets dragged backwards by the acceleration, so the artificial horizon will be a little bit below the true forward horizon for a while thereafter. The averaging time for a typical instrument is about five minutes. When the instrument gets old, its memory gets shorter because the gyro isn't spinning as fast, so the errors become larger.

19.10.3 Rate-of-Turn Gyro

There are two slightly different types of rate-of-turn gyro: (a) the rate-of-turn needle, and (b) the turn coordinator.

In both cases, the gyro is not free; it is a rate gyro. That is, its axis of rotation is more-or-less firmly attached to the airplane. It does not have gimbals. It is forced to change orientation when the airplane yaws, i.e. rotates around its Z axis.¹⁶ The instrument measures how much torque is required to re-orient the gyro.

Sometimes the rate-of-turn needle is built with its spin axis running parallel to the Y axis, in which case the airplane's yawing motion requires a torque around the X axis. Other models have the spin axis in the X direction, in which case yaw requires a torque around the Y axis. In principle, you could use any pair of axes that lie in the XY plane.¹⁷

The required torque is proportional to (a) the rate of change of orientation, and (b) the angular momentum of the gyro. Therefore an accurate rate-of-turn gyro must spin at exactly the right speed, not too fast or too slow. (This is in contrast to the directional gyro and the artificial horizon gyro, which just have to spin ``fast enough''.)

Many rate gyros incorporate a sneaky trick. They spin around the Y axis, with the top of the gyro spinning toward the rear. That is, the angular momentum vector points in the +Y direction. They also use a spring that is weak enough to allow the gyro to precess a little around the X axis. In a turn to the left, precession will tilt the gyro a little to the right. That means that during a turn, the gyro's tilt compensates for the airplane's bank, leaving the gyro somewhat more aligned with the earth's vertical axis. The goal, apparently, is to create an instrument that more nearly indicates heading change (relative to the earth's vertical axis) rather than simply rotation around the airplane's Z axis. Since the relationship between bank angle and rate of turn depends on airspeed, load factor, et cetera, this trick can't possibly achieve the goal except under special conditions.

The turn coordinator is very similar to the rate-of-turn needle. It displays a miniature airplane instead of a needle. The key operational difference is that it is slightly sensitive to rate of roll as well as rate of heading change. To create such an instrument, all you have to do is take a rate-of-turn instrument, tilt the mechanism nose-up by 20 or 30 degrees, and change the display.

The advantage of a turn coordinator is that it helps you anticipate what actions you need to take. That is, if the airplane has its wings level but is rolling to the right, it will probably be turning to the right pretty soon, so you might want to apply some aileron deflection. The disadvantage has to do with turbulence. Choppy air oftentimes causes the airplane to roll continually left and right. The roll rate can be significant, even if the bank angle never gets very large. The chop has relatively little effect on the yaw axis. In such conditions a plain old rate-of-turn needle gives a more stable indication than a turn coordinator does.

It is rather unfortunate that the display on a turn coordinator is a miniature airplane that banks left and right. This leads some people to assume, incorrectly, that the instrument indicates bank angle, which it most definitely does not.

1: This is traditionally expressed in terms of an ``action'' and an ``equal and opposite reaction'', but the meaning of those words has drifted over the centuries. Momentum is the modern term.
2: Troublemakers sometimes point out that lift actually is slightly reduced in a steady descent, since part of the weight is being supported by drag. To this I retort: (a) this is an obscure technicality, based on details of the definitions of the four forces (as given in section 4.1); (b) the magnitude of the reduction is negligible in ordinary flying, (c) the lift is reduced for climbs as well as descents — so this technicality certainly does not explain the motion, and (d) when we consider the total upward force, there is no reduction.
3: It is easy to find hand-waving explanations of the Coriolis effect that overlook one or the other of the two contributions, and are therefore off by a factor of two. Beware.
4: If you consider multiple widely-separated points, you can distinguish gravity versus centrifugity versus straight-line acceleration by checking for nonuniformities in the fields. However, an airplane is so small compared to the planet, and so small compared to its turning radius, that these nonuniformities do not provide a very practical way of telling one field from another.
5: It might be relevant if you are designing an airplane or a flight simulator.
6: In ordinary cases (specifically, when you know the forces are in balance and you are trying to figure out whether the torques are in balance) it doesn't matter what point in the airplane you choose as the pivot-point, provided you measure all lever arms from the same point.
7: Contrast this with the dot product used in section 4.4.
8: Sometimes you see these written as hyphenated words (foot-pounds or newton-meters) in which case the hyphen should not be mistaken for a minus sign. A foot-pound is a foot times a pound, not a foot minus a pound.
9: It is best to feed the string through a small smooth tube, rather than just your bare hand. You might use a poultry baster, or the axial hole in a spool of thread.
10: The bean-bag acquires the necessary straight-line momentum, and energy, via the string. It cannot acquire angular momentum from the string, since that would require a lever arm perpendicular to the force. Since the string can only exert a force parallel to itself, the lever arm is zero, so the torque is zero.
11: For an object rotating around an axis of symmetry, the angular momentum is exactly aligned with the axis; for an oddball axis this might not be true.
12: The word ``motion'' here refers to moving or re-orienting the airplane as a whole, not to the rotation of the propeller.
13: If you use your right hand, as shown, the torque vector is pointed in the direction of your thumb. Engineers would call this a negative pitching moment, since the torque vector points opposite to the standard (left to right) direction of the pitch axis.
14: An even fancier inertial platform would keep a position (not just orientation) independent of straight-line accelerations.
15: See figure 19.9 for the definition of the X, Y, and Z directions.
16: The instrument is not directly sensitive to any change in the direction the airplane is going, just to changes in the direction it is pointing.
17: The X, Y, and Z directions are defined in figure 19.9.

[Previous] [Contents] [Next]
[Comments or questions]