[Previous] [Contents] [Next]
[Comments or questions]

3 Airfoils and Airflow

—: Have you heard how to make a small fortune in the aviation business?
—: Start with a large one.

3.1 Flow Patterns Near a Wing

In this chapter I will explain a few things about how air behaves as it flows past a wing. There will be lots of illustrations, such as figure 3.1, produced by a wind-tunnel simulation¹ program that I wrote for my computer. The wing is stationary in the middle of the wind tunnel; air flows past it from left to right. A little ways upstream of the wing (near the left edge of the figure) I have arranged a number of smoke injectors. Seven of them are on all the time, injecting thin streams of purple smoke. The smoke is carried past the wing by the airflow, making visible stream lines.

Figure 3.1: Flow Past a Wing

In addition, on a five-times closer vertical spacing, I inject pulsed streamers. The smoke is turned on for 10 milliseconds out of every 20. In the figure, the blue smoke was injected starting 70 milliseconds ago, the green smoke was injected starting 50 milliseconds ago, the orange smoke was injected starting 30 milliseconds ago, and the red smoke was injected starting 10 milliseconds ago. The injection of the red smoke was ending just as the snapshot was taken.

The set of all points that passed the injector array at a given time defines a timeline. The right-hand edge of the orange smoke is the ``30 millisecond'' timeline.

Figure 3.2: Upwash and Downwash

Figure 3.2 points out some important properties of the airflow pattern. For one thing, we notice that the air just ahead of the wing is moving not just left to right but also upward; this is called upwash. Similarly, the air just aft of the wing is moving not just left to right but also downward; this is called downwash. Downwash behind the wing is relatively easy to understand; the whole purpose of the wing is to impart some downward motion to the air.

The upwash in front of the wing is a bit more interesting. As discussed in section 3.6, air is a fluid, which means it can exert pressure on itself as well as other things. The air pressure strongly affects the air, even the air well in front of the wing.

Along the leading edge of the wing there is something called a stagnation line, which is the dividing line between air that flows over the top of the wing and air that flows under the bottom of the wing. On an airplane, the stagnation line runs the length of the wingspan, but since figure 3.2 shows only a cross section of the wing, all we see of the stagnation line is a single point.

Another stagnation line runs spanwise along the trailing edge. It marks the place where air that passed above the wing rejoins air that passed below the wing.

We see that at moderate or high angles of attack, the forward stagnation line is found well below and aft of the leading edge of the wing. The air that meets the wing just above the stagnation line will backtrack toward the nose of the airplane, flow up over the leading edge, and then flow aft along the top of the wing.

Figure 3.3: Velocity Field of a Wing

Figure 3.3 introduces some additional useful concepts. Since the air near the wing is flowing at all sorts of different speeds and directions, the question arises of what is the ``true'' airspeed in the wind tunnel. The logical thing to do is to measure the velocity of the free stream; that is, at a point well upstream, before it has been disturbed by the wing.

The pulsed streamers give us a lot of information. Regions where the pulsed streamers have been stretched out are high velocity regions. This is pretty easy to see; each pulsed streamer lasts exactly 10 milliseconds, so if it covers a long distance in that time it must be moving quickly. The maximum velocity produced by this wing at this angle of attack is about twice the free-stream velocity. Airfoils can be very effective at speeding up the air.

Conversely, regions where the pulsed streamers cover a small distance in those 10 milliseconds must be low-velocity regions. The minimum velocity is zero. That occurs near the front and rear stagnation lines.

The relative wind vanishes on the stagnation lines. A small bug walking on the wing of an airplane in flight could walk along the stagnation line without feeling any wind.²

Stream lines have a remarkable property: the air can never cross a stream line. That is because of the way the stream lines were defined: by the smoke. If any air tried to flow past a point where the smoke was, it would carry the smoke with it. Therefore a particular parcel of air bounded by a pair of stream lines (above and below) and a pair of timelines (front and rear) never loses its identity. It can change shape, but it cannot mix with another such parcel.³

Another thing we should notice is that in low velocity regions, the stream lines are farther apart from each other. This is no accident. At reasonable airspeeds, the wing doesn't push or pull on the air hard enough to change its density significantly (see section 3.4.3 for more on this). Therefore the air parcels mentioned in the previous paragraph do not change in area when they change their shape. In one region, we have a long, skinny parcel of air flowing past a particular point at a high velocity. (If the same amount of fluid flows through a smaller region, it must be flowing faster.) In another region, we have a short fat parcel flowing by at a low velocity.

The most remarkable thing about this figure is that the blue smoke that passed slightly above the wing got to the trailing edge 10 or 15 milliseconds earlier than the corresponding smoke that passed slightly below the wing.

This is not a mistake. Indeed, we shall see in section 3.10.3 that if this were not true, it would be impossible for the wing to produce lift.

This may come as a shock to many readers, because all sorts of standard references claim that the air is somehow required to pass above and below the wing in the same amount of time. I have seen this erroneous statement in elementary-school textbooks, advanced physics textbooks, encyclopedias, and well-regarded pilot training handbooks. Bear with me for a moment, and I'll convince you that figure 3.3 tells the true story.

First, I must convince you that there is no law of physics that prevents one bit of fluid from being delayed relative to another.

Figure 3.4: Delay is Not Forbidden

Consider the scenario depicted in figure 3.4. A river of water is flowing left to right. Using a piece of garden hose, I siphon some water out of the river, let it waste some time going through several feet of coiled-up hose, and then return it to the river. The water that went through the hose will be delayed. The delayed parcel of water will never catch up with its former neighbors; it will not even try to catch up.

Note that delaying the water did not require compressing the water, nor did it require friction.

The same story applies to air. Air flowing past an obstacle will be delayed. In fact, air that comes arbitrarily close to a stagnation line will be delayed an arbitrarily long time. The air molecules just hang around in the vicinity of the stagnation line, like the proverbial mule midway between two bales of hay, unable to decide which alternative to choose. This delay occurs even when the wing is producing zero lift, as shown in the top panel of figure 3.5.

You can see that in all cases the air that hit the stagnation line dead-on — the middle blue streamer — never makes it to the trailing edge in any of these figures.

When a wing is not producing lift⁴ it is just a slight obstacle to the airflow. Air passing near the wing is slightly delayed, but that's about all. Air that passed slightly above the wing is delayed about the same amount as the corresponding air that passed below the wing.

When the wing is producing lift, the airflow patterns become much more interesting, as you can see from the other panels of figure 3.5.

Figure 3.5: Airflow at Various Angles of Attack

Air that passes above the wing reaches the trailing edge substantially earlier than it would have if the wing had not been producing lift (except for a tiny parcel of air, invisible in the picture, that just barely missed the stagnation line). Air that passes below the wing is substantially delayed. These effects extend for quite a distance above and below the wing.

A wing (when it is producing lift) is amazingly effective at speeding up the air above it. Even though the air that passes above the wing has a longer path, it gets to the back earlier than the corresponding air that passes below the wing.

The change in speed is only temporary. As the air reaches the trailing edge and thereafter, it quickly returns to its original, free-stream velocity (plus a slight downward component). This can been seen in the figures, such as figure 3.3 — the spacing between successive smoke pulses returns to its original value.

The change in relative position is permanent. If we follow the air far downstream of the wing, we find that the air that passed below the wing will never catch up with the corresponding air that passed above the wing. It will not even try to catch up.

3.2 Pressure Patterns Near a Wing

Figure 3.6 is a contour plot that shows what the pressure is doing in the vicinity of the wing. All pressures will be measured relative to the ambient atmospheric pressure in the free stream. The blue-shaded regions indicate suction, i.e. negative pressure relative to ambient, while the red-shaded regions indicate positive pressure relative to ambient. The dividing line between pressure and suction is also indicated in the figure.

Figure 3.6: Pressure Near a Wing

The pressure and suction created by the wing are conveniently measured in multiples of the dynamic pressure.⁵ It is usually represented by the symbol Q. For a typical general-aviation flight situation, Q is about half a pound per square inch. The maximum positive pressure on the airfoil is exactly equal to Q; this occurs right at the stagnation lines.⁶ The maximum suction depends on the angle of attack, and on the detailed shape of the airfoil; for the situation in figure 3.6 the max suction is just over 0.8 Q. Each contour in the figure represents exactly 0.2 Q (roughly 0.1 psi).

There is a lot we can learn from studying this figure. For one thing, we see that the front quarter or so of the wing does half of the lifting. Another thing to notice is that suction acting on the top of the wing is vastly more important than pressure acting on the bottom of the wing. In figure 3.6, the wing is flying at an angle of attack of 3 degrees, a reasonable ``cruise'' value.

At this angle of attack, there is almost no high pressure on the bottom of the wing; indeed there is mostly suction there. The only reason the wing can support the weight of the airplane is that there is more suction on the top of the wing. (There is a tiny amount of positive pressure on the rear portion of the bottom surface, but the fact remains that suction above the wing does more than 100% of the job of lifting the airplane.)⁷

Once again, this pressure pattern would be really hard to explain in terms of bullets bouncing off the wing. Remember, the air is a fluid. It has a well-defined pressure everywhere in space. When this pressure field meets the wing, it exerts a force: pressure times area equals force.

At higher angles of attack, above-atmospheric pressure does develop below the wing, but it is always less pronounced than the below-atmospheric pressure above the wing.

3.3 Stream Line Curvature

Figure 3.7 shows what happens near the wing when we change the angle of attack. You can see that as the velocity changes, the pressure changes also.

Figure 3.7: Airflow and Pressure Near Wings

It turns out that given the velocity field, it is rather straightforward to calculate the pressure field. Indeed there are two ways to do this; we discuss one of them here, and the other in section 3.4.

We know that air has mass. Moving air has momentum. If the air parcel follows a curved path, there must be a net force on it, as required by Newton's laws.⁸

Pressure alone does not make a net force; you need a pressure difference so that one side of the air parcel is being pressed harder than the other. Therefore the rule is this: If at any place the stream lines are curved, the pressure at nearby places is different.

You can see in the figures that tightly-curved streamlines correspond to big pressure gradients and vice versa.

If you want to know the pressure everywhere, you can start somewhere and just add up all the changes as you move from place to place to place. This is mathematically tedious, but it works. It works even in situations where Bernoulli's principle isn't immediately applicable.

3.4 Bernoulli's Principle

We now discuss a second way in which pressure is related to velocity, namely Bernoulli's principle. In situations where this principle can be applied (which includes most situations), this is by far the slickest way to do it.

Bernoulli's principle is derived from the law of conservation of energy. It involves the kinetic energy of moving air and the potential energy stored in the ``springiness'' of the air. Just as energy can be stored in a wound-up spring, energy is stored in pressurized air.

Pressure, denoted P, is (by definition) a force per unit area, which is the same thing as an energy per unit volume:⁹

P = Potential Energy per volume (3.1)

Meanwhile, moving air contains kinetic energy just like any other moving object:

½ rv² = Kinetic Energy per volume (3.2)

where v is the local velocity, and r (the Greek letter ``rho'') is the density, i.e. the mass per unit volume.

Note: In your browser, the following should look like Greek letters: ``gp''. If they look like ``gamma'' and ``pi'' then all is well. If they look like Roman letters such as ``g'' and ``p'' then your browser has not properly loaded the symbol fonts. To fix this please refer to the font-fixing notes.

Combining these, we conclude:

P + ½ rv² = Mechanical Energy per volume (3.3)

Next, we make the approximation that we can ignore non-mechanical forms of energy (such as chemical reactions or heat produced by friction), and that we are not adding energy to the air using pumps, pistons, or whatever. Then, using the law that total energy cannot change (see chapter 1), we conclude that a given air parcel's mechanical energy remains constant as it flows past the wing.

Now, if the right-hand side of equation 3.3 is a constant, it tells us that whenever a given parcel of air increases its velocity, it must decrease its pressure, and vice versa. This relationship is called Bernoulli's principle.

Higher velocity means lower pressure, and vice versa
(assuming constant mechanical energy).

Oftentimes¹⁰ it turns out that all the air parcels start out with the same mechanical energy. In such a case we can even make a Bernoulli-like statement comparing different parcels of air: Any fast-moving air must have lower pressure than any slow-moving air with the same mechanical energy.

Bernoulli's principle cannot be trusted if processes other than kinetic energy and pressure energy are important. In particular, in the ``boundary layer'' very near the surface of a wing, energy is constantly being dissipated (converted to heat) by friction. Fortunately, the boundary layer is usually very thin (except near the stall), and if we ignore it entirely Bernoulli's principle gives essentially the right answer.

3.4.1 Magnitude

It makes sense to measure the local velocity (lower-case v) at each point as a multiple of the free-stream velocity (capital V) since they vary in proportion to each other. Similarly it makes sense to measure relative pressures in terms of the dynamic pressure:

Q = ½ rV² (3.4)

which is always small compared to atmospheric pressure (assuming V is small compared to the speed of sound). The pressure versus velocity relationship is shown graphically in figure 3.8. The highest possible pressure (corresponding to completely stopped air) is one Q above atmospheric, while fast-moving air can have pressure several Q below atmospheric.

It doesn't matter whether we measure P as an absolute pressure or as a relative pressure (relative to atmospheric). If you change from absolute to relative pressure it just shifts both sides of Bernoulli's equation by a constant, and the new value (just as before) remains constant as the air parcel flows past the wing. Similarly, if we use relative pressure in figure 3.8, we can drop the word ``Atm'' from the pressure axis and just speak of ``positive one Q'' and ``negative two Q'' — keeping in mind that all the pressures are only slightly above or below one atmosphere.

Figure 3.8: Pressure versus Velocity

Bernoulli's principle allows us to understand why there is a positive pressure bubble right at the trailing edge of the wing (which is the last place you would expect if you thought of the air as a bunch of bullets). The air at the stagnation line is the slowest-moving air in the whole system; it is not moving at all. It has the highest possible pressure, namely Atm + Q.

As we saw in the bottom panel of figure 3.7, at high angles of attack a wing is extremely effective at speeding up the air above the wing and retarding the air below the wing. The maximum local velocity above the wing can be more than twice the free-stream velocity. This creates a negative pressure (suction) of more than 3 Q.

3.4.2 Altimeters; Static versus Stagnation Pressure

Consider the following line of reasoning:

The airplane's altimeter operates by measuring the pressure at the static port.
The static port is oriented sideways to the airflow, at a point chosen so that the air flows past with a local velocity just equal to the free-stream velocity.
In accordance with Bernoulli's principle, this velocity must be associated with a ``lower'' pressure there.
You might think this lower pressure would cause huge errors in the altimeter, depending on airspeed. In fact, though, there are no such errors. The question is, why not?

The answer has to do with the notion of ``lower'' pressure. You have to ask, lower than what? Indeed the pressure there is 1 Q lower than the mechanical energy (per unit volume) of the air. However, in your reference frame, the mechanical energy of the air is 1 Atm + 1 Q. When we subtract 1 Q from that, we see that the pressure in the static port is just equal to atmospheric. Therefore the altimeter gets the right answer, independent of airspeed.

Another way of saying it is that the air near the static port has 1 Atm of potential energy (pressure) and 1 Q of kinetic energy.

In contrast, the air in the Pitot tube has the same mechanical energy, 1 Atm + 1 Q, but it is all in the form of potential energy since (in your reference frame) it has no kinetic energy.

The mechanical energy per unit volume is officially called the stagnation pressure, since it is the pressure that you observe in the Pitot tube or any other place where the air is stagnant, i.e. where the local velocity v is zero (relative to the airplane).

In ordinary language ``static'' and ``stagnant'' mean almost the same thing, but in aerodynamics they designate two very different concepts. The static pressure is the pressure you would measure in the reference frame of the air, for instance if you were in a balloon comoving with the free stream. As you increase your airspeed, the stagnation pressure goes up, but the static pressure does not.

Also: we can contrast this with what happens in a carburetor. There is no change of reference frames, so the mechanical energy (per unit volume) remains 1 Atm. The high-speed air in the throat of the Venturi has a pressure below the ambient atmospheric pressure.

3.4.3 Compressibility

First, a bit of terminology:

Pressure denotes a force per unit area.
Compressibility denotes a change in density in response to pressure.

Non-experts may not make much distinction between a ``pressurized'' fluid and a ``compressed'' fluid, but in the engineering literature there is a world of difference between the two concepts.

Every substance on earth is compressible — be it air, water, cast iron, or anything else. It must increase its density when you apply pressure; otherwise there would be no way to balance the energy equations.

However, changes in density are not very important to understanding how wings work, as long as the airspeed is not near or above the speed of sound. Typical general aviation airspeeds correspond to Mach 0.2 or 0.3 or thereabouts (even when we account for the fact that the wing speeds up the air locally), and at those speeds the density never changes more than a few percent.

For an ideal gas, density is proportional to pressure, so you may be wondering why pressure-changes are important but density-changes are not. Here's why:

Lift depends on a pressure difference between the top and bottom of the wing. Similarly pressure drag depends on pressure differences. Therefore the relevant differential pressures are zero plus important terms proportional to ½ rV².
Meanwhile, the density is some big number plus or minus unimportant terms proportional to ½ rV².

To say it again: Flight depends directly on total density but not directly on total atmospheric pressure, just pressure differences.

Many books say the air is ``incompressible'' in the subsonic regime. That's bizarrely misleading. In fact, when those books use the words ``incompressible flow'' it generally means that the density undergoes only small-percentage changes. This has got nothing to do with whether the fluid has a high or low compressibility. The real explanation is that the density-changes are small because the pressure-changes are small compared to the total atmospheric pressure.

Similarly, many books say that equation 3.3 only applies to an ``incompressible'' fluid. Again, that's bizarrely misleading. Here's the real story:

Compressibility specifies to first order how density depends on pressure. Equation 3.1 specifies to first order how the energy depends on pressure. It already accounts for the effects of compressibility and all other first-order quantities. Therefore equation 3.3 is valid whenever the pressure-changes are a small percentage of the total pressure, regardless of compressibility.
At high airspeeds, the pressure changes are bigger, and you need a more sophisticated form of Bernoulli's equation. As shown below, it is straightforward to include second-order terms — which, by the way, don't depend on compressibility, either. Indeed you can use the full equation of state, to derive Bernoulli's equation in a form that is valid even for large-percentage changes in pressure. See reference 2, page 29, equation 11.

Here is Bernoulli's equation including the second-order term. I have rewritten it in terms of energy per mass (rather than energy per volume), to make it clear that compression doesn't matter, since a parcel's mass doesn't change even if its volume changes:

r₀

[1 -

2 g

P - Atm

Atm

] + ½ v² = Mechanical Energy per mass (3.5)

where r₀ is the density of air at atmospheric pressure, and where g (gamma) is a constant that appears in the equation of state for the fluid. Its value ranges from 1.666 for helium, to 1.4 for air, to 1.0 for cool liquid water. It's ironic that the correction is actually smaller for air (which has a high compressibility) than it is for water (which has a much lower compressibility). So don't let anybody tell you that Bernoulli's principle can't account for compressibility. It already does, even in its simplest form.

3.5 Stall Warning Devices

We are now in a position to understand how stall warning devices work. There are two types of stall-warning devices commonly used on light aircraft. The first type (used on most Pipers, Mooneys, and Beechcraft) uses a small vane mounted slightly below and aft of the leading edge of the wing as shown in the left panel of figure 3.9. The warning is actuated when the vane is blown up and forward. At low angles of attack (e.g. cruise) the stagnation line is forward of the vane, so the vane gets blown backward and everybody is happy. As the angle of attack increases, the stagnation line moves farther and farther aft underneath the wing. When it has moved farther aft than the vane, the air will blow the vane forward and upward and the stall warning will be activated.

The second type of stall-warning device (used on the Cessna 152, 172, and some others, not including the 182) operates on a different principle. It is sensitive to suction at the surface rather than flow along the surface. It is positioned just below the leading edge of the wing, as indicated in the right panel of figure 3.9. At low angles of attack, the leading edge is a low-velocity, high-pressure region; at high angles of attack it becomes a high-velocity, low-pressure region. When the low-pressure region extends far enough down around the leading edge, it will suck air out of the opening. The air flows through a harmonica reed, producing an audible warning.

Figure 3.9: Stall Warning Devices

Note that neither device actually detects the stall. Each one really just measures angle of attack. It is designed to give you a warning a few degrees before the wing reaches the angle of attack where the stall is expected. Of course if there is something wrong, such as frost on the wing (see section 3.13), the wing will stall at a lower-than-expected angle of attack, and you will get no warning from the so-called stall warning device.

3.6 Air Is A Fluid, Not A Bunch of Bullets

We all know that at the submicroscopic level, air consists of particles, namely molecules of nitrogen, oxygen, water, and various other substances. Starting from the properties of these molecules and their interactions, it is possible to calculate macroscopic properties such as pressure, velocity, viscosity, speed of sound, et cetera.

However, for ordinary purposes such as understanding how wings work, you can pretty much forget about the individual particles, since the relevant information is well summarized by the macroscopic properties of the fluid. This is called the hydrodynamic approximation.

In fact, when people try to think about the individual particles, it is a common mistake to overestimate the size of the particles and to underestimate the importance of the interactions between particles.

Figure 3.10: The Bullet Fallacy

If you erroneously imagine that air particles are large and non-interacting, perhaps like the bullets shown in figure 3.10, you will never understand how wings work. Consider the following comparisons. There is only one important thing bullets and air molecules have in common:

Bullets hit the bottom of the wing, transferring upward momentum to it.

Similarly, air molecules hit the bottom of the wing, transferring upward momentum to it.

Otherwise, all the important parts of the story are different:

No bullets hit the top of the wing.

Air pressure on top of the wing is only a few percent lower than the pressure on the bottom.

The shape of the top of the wing doesn't matter to the bullets.

The shape of the top of the wing is crucial. A spoiler at location ``X'' in figure 3.10 could easily double the drag of the entire airplane.

The bullets don't hit each other, and even if they did, it wouldn't affect lift production.

Each air molecule collides with one or another of its neighbors 10,000,000,000 times per second. This is crucial.

Each bullet weighs a few grams.

Each nitrogen molecule weighs 0.00000000000000000000005 grams.

Bullets that pass above or below the wing are undeflected.

The wing creates a pressure field that strongly deflects even far-away bits of fluid.

Bullets could not possibly knock a stall-warning vane forward.

Fluid flow nicely explains how such a vane gets blown forward and upward. See section 3.5.

The list goes on and on, but you get the idea. Interactions between air molecules are a big part of the story. It is a much better approximation to think of the air as a continuous fluid than as a bunch of bullet-like particles.

3.7 Other Fallacies

You may have heard stories that try to use the Coanda effect or the teaspoon effect to explain how wings produce lift. These stories are completely fallacious, as discussed in section 18.4.4 and section 18.4.3.

There are dozens of other fallacies besides. It is beyond the scope of this book to discuss them, or even to catalog them all.

3.8 Inverted Flight, Cambered vs. Symmetric Airfoils

Almost everybody has been told that an airfoil produces lift because it is curved on top and flat on the bottom. But aren't you also aware that airshow pilots routinely fly for extended periods of time upside down? Doesn't that make you suspicious that there might be something wrong with the story about curved on top and flat on the bottom?

Here is a list of things you need in an airplane intended for upside-down flight:

You need super-duper seatbelts to keep the pilot from flopping around.
You need to make sure the airframe is strong enough to withstand extra stress, including stress in new directions.
You need to make sure that the fuel, engine oil, and battery acid stay where they are supposed to be.

You will notice that changing the cross-sectional shape of the wing is not on this list. As shown in figure 3.11, an ordinary wing flies just fine inverted. It looks rather peculiar flying with the flat surface on top and the rounded surface on the bottom, but it works.

Figure 3.11: Inverted Flight

The common misconception that wings must be curved on top and flat on the bottom is related to the previously-discussed misconception that the air is required to pass above and below the wing in equal amounts of time. In fact, an upside-down wing produces lift by exactly the same principle as a rightside-up wing.

Figure 3.12: Airfoil Terminology

To help us discuss airfoil shapes, figure 3.12 illustrates some useful terminology.

The chord line is the straight line drawn from the leading edge to the trailing edge.
The term camber in general means ``bend''. If you want to quantify the amount of camber, draw a curved line from the leading edge to the trailing edge, staying always halfway between the upper surface and the lower surface; this is called the mean camber line. The maximum difference between this and the chord line is the amount of camber. It can be expressed as a distance or (more commonly) as a percentage of the chord length.

A symmetric airfoil, where the top surface is a mirror image of the bottom surface, has zero camber. The airflow and pressure patterns for such an airfoil are shown in figure 3.13.

Figure 3.13: Symmetric Airfoil

This figure could be considered the side view of a symmetric wing, or the top view of a rudder. Rudders are airfoils, too, and work by the same principles.

At small angles of attack, a symmetric airfoil works better than a highly cambered airfoil. Conversely, at high angles of attack, a cambered airfoil works better than the corresponding symmetric airfoil. An example of this is shown in figure 3.14. The airfoil designated ``631-012'' is symmetric, while the airfoil designated ``631-412'' airfoil is cambered; otherwise the two are identical.¹¹ At any normal angle of attack (up to about 12 degrees), the two airfoils produce virtually identical amounts of lift. Beyond that point the cambered airfoil has a big advantage because it does not stall until a much higher relative angle of attack. As a consequence, its maximum coefficient of lift is much greater.

Figure 3.14: Camber Fends Off The Stall

At high angles of attack, the leading edge of a cambered wing will slice into the wind at less of an angle compared to the corresponding symmetric wing. This doesn't prove anything, but it provides an intuitive feeling for why the cambered wing has more resistance to stalling.

The amount of camber on a typical modern airfoil is only 1 or 2 percent — obviously not crucial. One reason wings are not more cambered is that any increase would require the bottom surface to be concave — which would be a pain to manufacture. Another reason is that large camber is only really beneficial near the stall — i.e. for takeoff and landing, and it suffices to create lots of camber by extending the flaps when needed.

Reverse camber is clearly a bad idea (since it causes earlier stall) so aircraft that are expected to perform well upside down (e.g. Pitts or Decathlon) have symmetric (zero-camber) airfoils.

We have seen that under ordinary conditions, the amount of lift produced by a wing depends on the angle of attack, but hardly depends at all on the amount of camber. This makes sense. In fact, the airplane would be unflyable if the coefficient of lift were determined solely by the shape of the wing. Since the amount of camber doesn't often change in flight, there would be no way to change the coefficient of lift. The airplane could only support its weight at one special airspeed, and would be unstable and uncontrollable. In reality, the pilot (and the trim system) continually regulate the amount of lift by regulating the all-important angle of attack; see chapter 2 and chapter 6.

3.9 Thin Wings

The wing used on the Wright brothers' first airplane is thin, highly cambered, and quite concave on the bottom. This is shown in figure 3.15. There is no significant difference between the top surface and the bottom surface — same length, same curvature. Still, the wing produces lift, using the same lift-producing principle as any other airfoil. This should further dispel the notion that wings produce lift because of a difference in length between the upper and lower surfaces.

Similar remarks apply to the sail of a sailboat. It is a very thin wing, oriented more-or-less vertically, producing sideways lift.

Figure 3.15: The Wrights' 1903 Airfoil

Even a thin flat object such as a barn door will produce lift, if the wind strikes it at an appropriate angle of attack. The airflow pattern (somewhat idealized) for a barn door (or the wing on a dime-store balsa glider) is shown in figure 3.16. Once again, the lift-producing mechanism is the same.

Figure 3.16: Barn Door — Natural Airflow

3.10 Circulation

3.10.1 Visualizing the circulation

You may be wondering whether the flow patterns shown in figure 3.16 or the earlier figures are the only ones allowed by the laws of hydrodynamics. The answer is: almost, but not quite. Figure 3.17 shows the barn door operating with the same angle of attack (and the same airspeed) as in figure 3.16, but the airflow pattern is different.

Figure 3.17: Barn Door — Unnatural Stream Lines

Figure 3.18: Barn Door — Pure Circulation

Figure 3.19: Barn Door — Natural Stream Lines

The new airflow pattern (figure 3.17) is highly symmetric. I have deleted the timing information, to make it clear that the stream lines are unchanged if you flip the figure right/left and top/bottom. The front stagnation line is a certain distance behind the leading edge; the rear stagnation line is the same distance ahead of the trailing edge. This airflow pattern produces no lift. (There will be a lot of torque — the so-called Rayleigh torque — but no lift.)

The difference between these figures is circulation — figure 3.16 has circulation while figure 3.17 does not. (Figure 3.19 is the same as figure 3.16 without the timing information.)

To understand circulation and its effects, first imagine an airplane with barn-door wings, parked on the ramp on a day with no wind. Then imagine stirring the air with a paddle, setting up a circulatory flow pattern, flowing nose-to-tail over the top of the wing and tail-to-nose under the bottom (clockwise in this figure). This is the flow pattern for pure circulation, as shown in figure 3.18. Then imagine that a headwind springs up (left to right in the figure). At each point in space, the velocity fields will add. The circulatory flow and the wind will add above the wing, producing high velocity and low pressure there. The circulatory flow will partially cancel the wind below the wing, producing low velocity and high pressure there.

If we take the noncirculatory left-to-right flow in figure 3.17 and add various amounts of circulation, we can generate all the flow patterns consistent with the laws of hydrodynamics — including the actual natural airflow shown in figure 3.16 and figure 3.19.¹²

There is nothing special about barn doors; real airfoils have analogous airflow patterns, as shown in figure 3.20, figure 3.21, and figure 3.22.

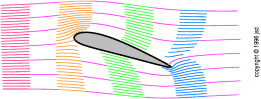Figure 3.20: Unnatural Airflow — Angle of Attack but No Circulation

Figure 3.21: Pure Circulation

Figure 3.22: Normal, Natural Airflow

If you suddenly accelerate a wing from a standing start, the initial airflow pattern will be noncirculatory, as shown in figure 3.20. Fortunately for us, the air absolutely hates this airflow pattern, and by the time the wing has traveled a short distance (a couple of chord-lengths or so) it develops enough circulation to produce the normal airflow pattern shown in figure 3.22.

3.10.2 How Much Circulation? The Kutta Condition

In real flight situations, precisely enough circulation will be established so that the rear stagnation line is right at the trailing edge, so no air needs to turn the corner there. Of course, the circulation that cancels the flow around the trailing edge more or less doubles the flow around the leading edge.

The general rule — called the Kutta condition — is that the air hates to turn the corner at a sharp trailing edge. To a first approxmation, the air hates to turn the corner at any sharp edge, because the high velocity there creates a lot of friction. For ordinary wings, that's all we need to know, because the trailing edge is the only sharp edge.

The funny thing is that the trailing edge is sharp, an airfoil will work even if the leading edge is sharp, too. This explains why dime-store balsa-wood gliders work, even with sharp leading edges.

It is a bit of a mystery why the air hates turning a corner at the trailing edge, and doesn't mind so much turning a sharp corner at the leading edge — but that's the way it is.¹³ This is related to the well-known fact that blowing is different from sucking. (Even though you can blow out a candle from more than a foot away, you cannot suck out a candle from more than an inch or two away.) In any case, the rule is:

The air wants to flow cleanly off the trailing edge.

As the angle of attack increases, the amount of circulation needed to meet the Kutta condition increases.

Here is a nice, direct way of demonstrating the Kutta condition: At a safe altitude, start with the airplane¹⁴ in the clean configuration in level flight, a couple of knots above the speed where the stall warning horn comes on. Maintaining constant pitch attitude and maintaining level flight, extend the flaps. The stall warning horn will come on. There is no need to stall the airplane; the warning horn itself makes the point.

This demonstration makes it clear that the flap (which is at the back of the wing) is having a big effect on the airflow around the entire wing, including the stall-warning detector (which is near the front).

Extending the flaps (while maintaining constant pitch and constant direction of flight) increases the angle of attack. This increases the circulation, which trips the stall-warning detector as described in section 3.5.

3.10.3 How Much Lift? The Kutta-Zhukovsky Theorem

Here is a beautifully simple and powerful result: The lift is equal to the airspeed, times the circulation, times the density of the air, times the span of the wing. This is called the Kutta-Zhukovsky theorem.

Lift = airspeed × circulation × density × span

Since circulation is proportional to the coefficient of lift and to the airspeed, this new notion is consistent with our previous knowledge that the lift should be proportional to the coefficient of lift times airspeed squared.

You can look at a velocity field and visualize the circulation. In figure 3.23, the vertical black line shows where the 70 millisecond timeline would have been if the wing had been completely absent. The actual 70 millisecond timeline is given by the right-hand edge of the blue streamers.

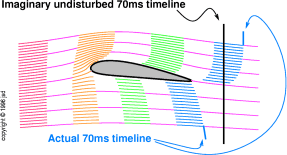Figure 3.23: Circulation Advances Upper & Retards Lower Streamers

Because of the circulatory contribution to the velocity, the streamers above the wing are at a relatively advanced position, while the streamers below the wing are at a relatively retarded position.

If you refer back to figure 3.7, you can see that circulation is proportional to angle of attack. In particular, note that when the airfoil is not producing lift there is no circulation — the upper streamers are not advanced relative to the lower streamers.

The same thing can be seen by comparing figure 3.20 to figure 3.22 — when there is no circulation the upper streamers are not advanced relative to the lower streamers.

3.10.4 Quantifying the Circulation

Circulation can be measured, according to the following procedure. Set up an imaginary loop around the wing. Go around the loop clockwise, dividing it into a large number of small segments. For each segment, multiply the length of that segment times the speed of the air along the direction of the loop at that point. (If the airflow direction is opposite to the direction of the loop, the product will be negative.) Add up all the products. The total velocity-times-length will be the circulation. This is the official definition.

Interestingly, the answer is essentially independent of the size and shape of the loop.¹⁵ For instance, if you go farther away, the velocity will be lower but the loop will be longer, so the velocity-times-length will be unchanged.

3.11 Mechanically-Induced Circulation

There is a widely-held misconception that it is the velocity relative to the skin of the wing that produces lift. This causes no end of confusion.

Remember that the air has a well defined velocity and pressure everywhere, not just at the surface of the wing. You can go anywhere near or far from the wing with a windmill and a pressure gauge and measure the velocity and pressure. The circulatory flow set up by the wing creates low pressure in a huge region extending far above the wing. The velocity at each point determines the pressure at that point.

The circulation near a wing is normally set up by the interaction of the wind with the shape of the wing. But there are other ways of setting up circulatory flow. In figure 3.24, the wings are not airfoil-shaped but paddle-shaped. By rotating the paddle-wings we can set up a circulatory airflow pattern by brute force.

Figure 3.24: Paddle-Wing Airplane

Bernoulli's principle would apply point by point in the air near the wing, creating low pressure that would pull up on the wings, even though the air near the wing would have no velocity relative to the wing since it would be ``stuck'' between the vanes of the paddle. The Kutta-Zhukovsky theorem would apply, as stated above: lift is equal to the airspeed, times the circulation, times the density of the air, times the span of the wing.

This phenomenon — creating the circulation needed for lift by mechanically stirring the air — is called the Magnus effect.

The airplane in figure 3.24 would have definite controllability problems, since the notion of angle of attack would not exist (see chapter 2 and chapter 6). The concept, though, is not as ridiculous as might seem. The famous aerodynamicist Flettner once built a ship that ``sailed'' all the way across the Atlantic using huge rotating cylinders rather than sails to catch the wind.

Also, it is easier than you might think to demonstrate this important concept. You don't need four vanes on the rotating paddle; a single flat surface will do. A business card works fairly well. Drop the card from shoulder height, with its long axis horizontal. As you release it, give it a little bit of backspin around the long axis. It will fly surprisingly well; the lift-to-drag ratio is not enormous, but it is not zero either. The motion is depicted in figure 3.25.

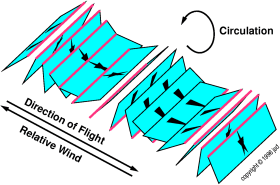Figure 3.25: Fluttering Card — Lift Created by Circulation

You can improve the performance by giving the wing a finer aspect ratio (more span and/or less chord). I once took a manila folder and cut out several pieces an inch wide and 11 inches long; they work great.

As an experiment, try giving the wing the wrong direction of circulation (i.e. topspin) as you release it. What do you think will happen?

I strongly urge you to try this demonstration yourself. It will improve your intuition about the relationship of circulation and lift.

Figure 3.26: Curve Balls

We can use these ideas to understand some (but not all) of the aerodynamics of tennis balls and similar objects. As portrayed in figure 3.26, if a ball is hit with a lot of backspin, the surface of the spinning ball will create the circulatory flow pattern necessary to produce lift, and it will be a ``floater''. Conversely, the classic ``smash'' involves topspin, which produces negative lift, causing the ball to ``fly'' into the ground faster than it would under the influence of gravity alone. Similar words apply to leftward and rightward curve balls.

To get even close to the right answer, we must ask where the relative wind is fast or slow, relative to the center of the ball — not relative to the rotating surface of the ball. Remember that the fluid has a velocity and a pressure everywhere, not just at the surface of the ball. Air moving past a surface is what creates drag, not lift. Bernoulli says that when an air parcel accelerates or decelerates, it exchanges its kinetic energy (airspeed) for potential energy (pressure). For the floater, the circulatory flow created by the backspin combines with the free-stream flow created by the ball's forward motion to create high-velocity, low-pressure air above the ball — that is, lift.

This simple picture of mechanically-induced circulation applies best to balls that have evenly-distributed roughness. Cricket balls are in a different category, since they have a prominent equatorial seam. If you spin-stabilize the orientation of the seam, and fly the seam at an ``angle of attack'', airflow over the seam causes extra turbulence which promotes attached flow on one side of the ball. See section 18.3 for some discussion of attached versus separated flow. Such effects can overwhelm the mechanically-induced circulation.

To really understand flying balls or cylinders, you would need to account for the direct effect of spin on circulation, the effect of spin on separation, the effect of seams on separation, et cetera. That would go beyond the scope of this book. A wing is actually easier to understand.

3.12 Lift Requires Circulation & Vortices

3.12.1 Vortices

A vortex is a bunch of air circulating around itself. The axis around which the air is rotating is called a vortex line. It is mathematically impossible for a vortex line to have loose ends. A smoke ring is an example of a vortex. It closes on itself so it has no loose ends.

The circulation necessary to produce lift can attributed to a bound vortex line. It binds to the wing and travels with the airplane. The question arises, what happens to this vortex line at the wingtips?

The answer is that the vortex spills off each wingtip. Each wing forms a trailing vortex (also called wake vortex) that extends for miles behind the airplane. These trailing vortices constitute the continuation of the bound vortex. See figure 3.27. Far behind the airplane, possibly all the way back at the place where the plane left ground effect, the two trailing vortices join up to form an unbroken vortex line.

Figure 3.27: Bound Vortex, Trailing Vortices

The air rotates around the vortex line in the direction indicated in the figure. We know that the airplane, in order to support its weight, has to yank down on the air. The air that has been visited by the airplane will have a descending motion relative to the rest of the air. The trailing vortices mark the boundary of this region of descending air.

It doesn't matter whether you consider the vorticity to be the cause or the effect of the descending air — you can't have one without the other.

Lift must equal weight times load factor, and we can't easily change the weight, or the air density, or the wingspan. Therefore, when the airplane flies at a low airspeed, it must generate lots of circulation.

* Winglets, etc.

It is a common misconception that the wingtip vortices are somehow associated with unnecessary spanwise flow, and that they can be eliminated using fences, winglets, et cetera. The reality is that the vortices are completely necessary; you cannot produce lift without producing vortices. By fiddling with the shape of the wing the designer can control where along the span the vortices are shed, but there is no way to get rid of the vorticity without getting rid of the lift.

Winglets encourage the vortices to be shed at the wingtips, not somewhere else along the span. This produces more lift, since it is only the amount of span that carries circulation that produces lift according to the Kutta-Zhukovsky theorem. Still, as a general rule, adding a pair of six-foot-tall winglets has no aerodynamic advantage compared to adding six feet of regular, horizontal wing on each side.¹⁶

The bound vortex that produces the circulation that supports the weight of the airplane should not be confused with the little vortices produced by vortex generators (to re-energize the boundary layer) as discussed in section 18.3.

3.12.2 Wake Turbulence

When air traffic control (ATC) tells you ``caution — wake turbulence'' they are really telling you that some previous airplane has left a wake vortex in your path. The wake vortex from a large, heavy aircraft can easily flip a small aircraft upside down.

A heavy airplane like a C5-A flying slowly is the biggest threat, because it needs lots of circulation to support all that weight at a low airspeed. You would think that a C5-A with flaps extended would be the absolute worst, but that is not quite true. The flaps do increase the circulation-producing capability of the wing, but they do not extend over the full span. Therefore a part of the circulation is shed where the flaps end, and another part is shed at the wingtips. If you fly into the wake of another plane, two medium-strength vortices will cause you less grief than a single full-strength vortex. Therefore, you should expect that the threat from wake vortices is greatest behind an airplane that is heavy, slow, and clean.

Like a common smoke ring, the wake vortex does not just sit there, it moves. In this case it moves downward. A common rule of thumb says they normally descend at about 500 feet per minute, but the actual rate will depend on the wingspan and coefficient of lift of the airplane that produced the vortex.

Vortices are part of the air; if the wind is blowing, the vortices will be carried downwind. In fact, the reason wake vortices descend is that the right vortex is carried downward by the flow field set up by the left vortex, and the left vortex is carried downward by the flow field set up by the right vortex. Superimposed on this flow field, the overall wind blows the vortices around in the obvious way.

When a vortex line gets close to the ground, it ``sees its reflection''. That is, it moves as if there were being acted on by a mirror-image vortex line a few feet below the ground. This causes wake vortices to spread out — the left vortex starts moving to the left, and the right vortex starts moving to the right.

* Avoiding Wake Turbulence Problems

If you are flying a light aircraft, avoid the airspace below and behind a large aircraft. Avoiding the area for a minute or two suffices, because a vortex that is older than that will have lost enough intensity that it is probably not a serious problem.

If you are landing on the same runway as a preceding large aircraft, you can avoid its wake vortices by flying a high, steep approach, and landing at a point well beyond the point where it landed. Remember, it doesn't produce vortices unless it is producing lift. Assuming you are landing into the wind, the wind can only help clear out the vortices for you.

If you are departing from the same runway as a preceding large aircraft, you can avoid its vortices — in theory — if you leave the runway at a point well before the point where it did, and if you make sure that your climb-out profile stays above and/or behind its. In practice, this might be hard to do, since the other aircraft might be able to climb more steeply than you can. Also, since you are presumably taking off into the wind, you need to worry that the wind might blow the other plane's vortices toward you.

A light crosswind might keep a vortex on the runway longer, by opposing its spreading motion. A less common problem is that a crosswind might blow vortices from a parallel runway onto your runway.

The technique that requires the least sophistication is to delay your takeoff a few minutes, so the vortices can spread out and be weakened by friction.

3.12.3 Induced Drag

Here are some more benefits of understanding circulation and vortices: it explains induced drag, and explains why gliders have long skinny wings. Induced drag is commonly said to be the ``cost'' of producing lift. But there is no law of physics that requires a definite cost. If you could take a very large amount of air and pull it downward very gently, you could support your weight at very little cost. The cost you absolutely must pay is the cost of making that trailing vortex. For every mile that the airplane flies, each wingtip makes another mile of vortex. The circulatory motion in that vortex involves nontrivial amounts of kinetic energy, and that's why you have induced drag. A long skinny wing will need less circulation than a short fat wing producing the same lift. Gliders (which need to fly slowly with minimum drag) therefore have very long skinny wings (limited only by strength; it's hard to build something long, skinny, and strong).

3.12.4 Soft-Field Takeoff

We can now understand why soft-field takeoff procedure works. When the aircraft is in ground effect, it ``sees its reflection'' in the ground. If you are flying 10 feet above the ground, the effect is the same as having a mirror-image aircraft flying 10 feet below the ground. Its wingtip vortices spin in the opposite direction and largely cancel your wingtip vortices — greatly reducing induced drag.

As discussed in section 13.4, in a soft-field takeoff, you leave the ground at a very low airspeed, and then fly in ground effect for a while. There will be no wheel friction (or damage) because the wheels are not touching the ground. There will be very little induced drag because of the ground effect , and there will be very little parasite drag because you are going slowly. The airplane will accelerate like crazy. When you reach normal flying speed, you raise the nose and fly away.

3.13 Frost on the Wings

The Federal Aviation Regulations prohibit takeoff when there is frost adhering to the wings or control surfaces, unless it is polished smooth.

It is interesting that they do not require it to be entirely removed, just polished smooth.

There are very good aerodynamic reasons for this rule:

The most obvious effect of roughness on the wings is to create a lot more drag, as seen in the right panel in figure 3.28, which shows wind-tunnel data for a real airfoil (the NACA 631-412 airfoil; see reference 5). At cruise angle of attack, the drag is approximately doubled; at higher angles of attack (corresponding to lower airspeeds) it is even worse.
The less obvious (yet more critical) problem is that roughness causes the wing to stall at a considerably lower angle of attack, lower coefficient of lift, and higher airspeed. This can be seen in the left panel of figure 3.28. The pilot of the frosty airplane could get a very nasty surprise.

Figure 3.28: Roughness Degrades Wing Performance

As mentioned in section 3.4, Bernoulli's principle cannot be trusted when energy is being removed from the system by friction. Frost, by sticking up into the breeze, is very effective in removing energy from the system. This tends to de-energize the boundary layer, leading to separation which produces the stall.¹⁷

It is interesting that at moderate and low angles of attack (cruise airspeed and above) the frost has hardly any effect on the coefficient of lift. This reinforces the point made in section 3.11 that the velocity of the air right at the surface, relative to the surface, is not what produces the lift.

Sometimes the air temperature is just above freezing, but due to history or due to radiative cooling, the skin of the airplane is much colder and covered with frost. A jug of warm water works wonders.

3.14 Consistent (Not Cumulative) Laws of Physics

We have seen that several physical principles are involved in producing lift. Each of the following statements is correct as far as it goes:

The wing produces lift ``because'' it is flying at an angle of attack.
The wing produces lift ``because'' of circulation.
The wing produces lift ``because'' of Bernoulli's principle.
The wing produces lift ``because'' of Newton's law of action and reaction.

We now examine the relationship between these physical principles. Do we get a little bit of lift because of Bernoulli, and a little bit more because of Newton? No, the laws of physics are not cumulative in this way.

There is only one lift-producing process. Each of the explanations itemized above concentrates on a different aspect of this one process. The wing produces circulation in proportion to its angle of attack (and its airspeed). This circulation means the air above the wing is moving faster. This in turn produces low pressure in accordance with Bernoulli's principle. The low pressure pulls up on the wing and pulls down on the air in accordance with all of Newton's laws.

3.15 Momentum in the Air

For an airplane in steady flight, the forces must balance. We know from the Newton's third law ¹⁸ that for every force there must be an equal and opposite force somewhere, but the special idea here is that there must be an equal and opposite force locally to maintain equilibrium.

The earth pulls down on the airplane (by gravity). This force is balanced locally because the air pulls up on the airplane (by means of pressure near the wings). Of course the same pressure that pulls up on the airplane pulls down on the air; this force is transmitted from one air parcel to another to another, all the way to the earth's surface. At the earth's surface, pressure pushes up on the air and pushes down on the earth. The downward force on the earth is just enough to balance the fact that the airplane is pulling up on the earth (by gravity).

Since force is just momentum per unit time, the same process can be described by a big ``closed circuit'' of momentum flow. The earth transfers downward momentum to the airplane (by gravity). The airplane transfers downward momentum to the air (by pressure near the wings). The momentum is then transferred from air parcel to air parcel to air parcel. Finally the momentum is transferred back to the earth (by pressure at the surface), completing the cycle.

You need to look at figure 3.27 to get the whole story. If you look only at things like figure 3.2, you will never understand how the momentum balance works, because that figure doesn't tell the whole story. You might be tempted to make the following erroneous argument:

In figure 3.2, there is some upward momentum ahead of the wing, and some downward momentum behind the wing.
As the wing moves along, it carries the pattern of upwash and downwash along with it.
Therefore the total amount of upward and downward momentum in the air is not changing as the wing moves along. No momentum is being transferred to the air. Therefore no lift is being produced. This is nonsense!

To solve this paradox, remember that figure 3.2 does not tell the whole story. It only shows the effects of the bound vortex that runs along the wing, and does not show the effects of the trailing vortices. That is, it is only valid relatively close to the wing and relatively far from the wingtips.

Look at that figure and choose a point, say, half a chord ahead of the wing. You will see that the air has some upward momentum at that point. All points above and below that point within the frame of the figure also have upward momentum. But it turns out that if you go up or down from that point more than a wingspan or so, you will find that all the air has downward momentum. This is caused by the trailing vortices, which induce a downward flow. Near the wing the bound vortex dominates, but if you go higher or lower the trailing vortices dominate.

In fact, if you add up all the momentum in an entire column of air, for any column ahead of the wing, you will find that the total vertical momentum is zero. The total effect of the trailing vortices exactly cancels the total effect of the bound vortex.

If you consider points directly ahead of the wing (not above or below), a slightly different sort of cancellation occurs. The effect of the trailing vortices is never enough to actually reverse the flow; there is always some upwash directly ahead of the wing, no matter far ahead. But the effect of the trailing vortices greatly reduces the magnitude, so the upwash pretty soon becomes negligible. This is why it is reasonable to speak of ``undisturbed'' air ahead of the airplane.

Behind the wing there is no cancellation of any kind; the downwash of the wing is only reinforced by the downward flow induced by the trailing vortices. There is plenty of downward momentum in any air column behind the wing.

The general rule is simple: There is downward momentum in any air column that passes through the vortex loop (which is shown in figure 3.27). There is no momentum in any air column that is ahead of the wing, outboard of the trailing vortices, or aft of the starting vortex.

So now we can understand the momentum balance: As the airplane flies along minute by minute, it imparts more and more downward momentum to the air, by enlarging the region of downward-moving air behind it.

3.16 Summary: How a Wing Produces Lift

A wing is very effective at changing the speed of the air. The air above is speeded up; the air below is slowed down. Each air parcel gets a temporary change in speed and a permanent offset in position.
Bernoulli's principle asserts that a given parcel of air has high velocity when it has low pressure, and vice versa.
Below-atmospheric pressure above the wing is much more pronounced than above-atmospheric pressure below the wing.
There is significant upwash ahead of the wing and even more downwash behind the wing.
The front stagnation line is well below and behind the leading edge.
The rear stagnation line is at or very near the trailing edge. The Kutta condition says the air wants to flow cleanly off the sharp trailing edge. This determines the amount of circulation.
An airfoil does not have to be curved on top and/or flat on the bottom in order to work. A rounded leading edge is a good idea, but even a barn door will fly.
Air passing above and below the wing does not do so in equal time. When lift is being produced, the air passes above the wing in substantially less time.
Lift is equal to circulation, times airspeed, times density, times wingspan.
Well below the stalling angle of attack, the coefficient of lift is proportional to the angle of attack; the circulation is proportional to the coefficient of lift times the airspeed.
Air is a fluid, not a bunch of bullets. The fluid has pressure and velocity everywhere, not just where it meets the surface of the wing.
There is downward momentum in any air column behind the wing. There is zero momentum in any air column ahead of the wing, outboard of the trailing vortices, or aft of the starting vortex.
Vortex lines cannot have loose ends; therefore you cannot produce lift without producing wake vortices.
Induced drag arises when you have low speed and/or short span, because you are visiting a small amount of air and yanking it down violently, producing strong wake vortices. In contrast there is very little induced drag when you have high speed and/or long span, because you are visiting a large amount of air, pulling it down gently, producing weak wake vortices.

1: These simulations are based on a number of assumptions, including that the viscosity is small (but not zero), the airspeed is small compared to the speed of sound, the airflow is not significantly turbulent, no fluid can flow through the surface of the wing, and the points of interest are close to the wing and not too close to either wingtip.
2: To be more precise: there is no wind in either of the two dimensions that show up in figure 3.3. There might be some flow in the third dimension (i.e. spanwise along the stagnation line) but that isn't relevant to the present discussion.
3: ... although for turbulent flow, the stream lines can get so tangled that they lose any useful meaning.
4: As discussed in section 2.2, I choose to measure angle of attack in such a way that this zero-lift condition corresponds to zero angle of attack, even for cambered wings.
5: This was defined in section 2.12; see also section 3.4.
6: By Bernoulli's principle, the slowest air has the highest pressure. At the stagnation lines, the air is stopped — which as slow as it can get! See section 3.4, especially figure 3.8.
7: Of course, if there were no atmospheric pressure below the wing, there would be no way to have reduced pressure above the wing. Fundamentally, atmospheric pressure below the wing is responsible for supporting the weight of the airplane. The point is that pressure changes above the wing are more pronounced than the pressure changes below the wing.
8: Newton's laws are discussed in section 19.1.
9: This is a first-order equation, valid whenever the pressure changes are a small percentage of the total atmospheric pressure. See discussion below.
10: ... but not always. See section 18.4 for a counterexample.
11: The airfoil designations aren't just serial numbers; the digits actually contain information about the shape of the airfoil. For details see reference 5.
12: We are still assuming negligible viscosity, small percentage pressure changes, no turbulence in the fluid, no fluid flowing through the surface of the wing, and a few other reasonable assumptions.
13: Actually, you never get 100% of the circulation predicted by the Kutta condition, especially for crummy airfoils like barn doors. For nice airfoils with a rounded leading edge, you get something like 99% of the Kutta circulation.
14: Choose an airplane where the stall warning indicator is on the flapped section of the wing. This includes the Cessna C-152 and C-172, but not the C-182. It includes most Mooneys and the Grumman Tiger, but excludes Piper Cherokees and the Beech Bonanza.
15: This assumes that the loop is big enough to include the places where circulation is being produced (i.e. the wing and the boundary layer).
16: However, the winglet solution may provide a practical advantage when taxiing and parking. This is why Boeing put winglets (instead of additional span) on the 747-400 — they wanted to be able to park in a standard slot at the airport.
17: Boundary layers, separation, etc. are discussed in more detail in section 18.3.
18: See section 19.1 for a discussion of the laws of motion.

[Previous] [Contents] [Next]
[Comments or questions]