[Previous] [Contents] [Next]
[Comments or questions]

6 Angle of Attack Stability, Trim, and Spiral Dives

Maintain thine airspeed,
lest the ground arise and smite thee.
— Aviation proverb.

This chapter discusses how you should use the trim wheel, how the airplane responds to changes (or attempted changes) in angle of attack, and how you should recover from a spiral dive.

6.1 The Basic Stability Principle

To control pitch attitude, conventional pilot technique is to push or pull on the yoke until the airplane is doing what you want, and then to use the trim wheel to ``trim off'' the yoke forces — thereby telling the airplane to remember that the current aircraft behavior is what you prefer.

But let's look into this a little more closely. What aspect of the behavior is the trim wheel supposed to ``remember''?

the preferred rate of climb?
the preferred pitch attitude?
the preferred airspeed?
the preferred angle of attack?

The last answer is far and away the best: the airplane is trimmed for a definite angle of attack. As we shall see, knowing this has important safely implications. Trim for angle of attack!

As discussed in section 2.12, the airspeed indicator is the closest thing you have to an angle-of-attack indicator in typical light aircraft; therefore at standard weight (and load factor), trimming for airspeed is almost as sensible as trimming for angle of attack.

Angle of attack stability is crucial to well-behaved flight. It can be achieved without any complicated moving parts; even a balsa-wood toy glider maintains a definite angle of attack. To see how it works, let's start by considering the forces on the teeter-totter shown in figure 6.1.

Figure 6.1: Balance Insensitive to Rainfall

In the top panel of the figure, we have an ordinary playground teeter-totter with two buckets of water on it. Each bucket contains a four-inch depth of water. The left bucket has half as much horizontal area, so it contains half as much volume as the right bucket. Since the smaller bucket is twice as far away from the pivot, the torque from the small bucket is just equal (and opposite) to the torque from the big bucket; all the torques cancel.¹

Now let's consider what happens if an inch of rain falls on our teeter-totter. The new situation is shown in the bottom panel of figure 6.1. In both buckets, the depth of water increases by one inch, and in both buckets this represents a 25% increase. The system remains in equilibrium.²

We now contrast this with the slightly different teeter-totter arrangement shown in figure 6.2. The initial situation is shown in the top panel. This time, the small-area bucket (the one on the left) is filled to a depth of only one inch. The other bucket is filled to a depth of four inches. In order to get things in balance, the large bucket must be moved much closer to the pivot — four times closer than it was previously, and all-in-all eight times closer than the small bucket.

Figure 6.2: Balance Sensitive to Rainfall

Let's consider what happens if an inch of rain falls on this new arrangement. Once again, the depth of water increases in both buckets by one inch. This still represents a 25% increase for the right-hand bucket, but it now represents a 100% increase in the left-hand bucket. The same additional depth has a disproportionate effect. The system is no longer in equilibrium; it will tilt down to the left.

You may be wondering what all this has to do with airplanes. Well, this sort of reasoning is exactly what is needed to explain the angle-of-attack stability of an airplane. The situation is shown in figure 6.3.

Figure 6.3: Aircraft Sensitive to Angle of Attack

In the top panel, the airplane is just cruising along in still air. The wing is flying at a normal cruise angle of attack (four degrees), while the tail is flying at a much lower angle of attack (only one degree). This is in analogy with the two buckets, one having four inches of water and the other having only one inch.³

The torques are in balance because the even though the tail is ``loafing'' (producing much less lift than it is capable of) it is much, much farther away from the pivot point. You can check the balance mathematically: the tail has one-quarter as much coefficient of lift and one-half as much area, but it has eight times as much lever arm — so all the torques cancel.

The bottom panel of figure 6.3 shows what happens if the airplane flies into an updraft. Because of the updraft, the relative wind is no longer coming from straight ahead, but is coming from a point one degree below the forward horizon. In the first instant after the airplane enters the updraft, the pitch attitude will not have changed (it won't have had time to change) so at least for a moment both the tail and wing will be flying at an angle of attack one degree higher than previously: two degrees and five degrees, respectively. This represents a 100% increase for the tail but only a 25% increase for the wing. This creates a pitching moment. The aircraft will pitch nose-down into the updraft. The pitch-axis torque budget will return to equilibrium only when the original angle of attack has been restored.

The same logic applies to any other situation where the airplane finds itself flying at an angle of attack different from its trimmed angle of attack. Any increase or decrease in angle of attack will have a disproportionate effect on the tail. The airplane will pitch up or down until it restores its trimmed angle of attack.

Angle of attack stability results from this simple principle: ``the thing in back flies at a lower angle of attack than the thing in front''. Aircraft designers have a special word for any situation where two airfoils have different angles of incidence, namely decalage,⁴ from the French word for ``shift'' or ``offset''.⁵ The more wing/tail decalage you have, the more vigorously the airplane will oppose any attempted deviation from its preferred angle of attack.

* Other Flying Objects Are Not Similar

This property of being trimmed for a particular angle of attack is truly remarkable. It is not shared by other so-called ``aerodynamic'' objects such as darts, arrows or bombs. They can't be trimmed for any angle of attack other than zero. If you drop a bomb from a great height, it will (to an excellent approximation) wind up pointing straight down and going straight down, with a velocity essentially as large as could possibly be obtained from an object of that size and weight. In contrast, an ordinary airframe in ordinary gliding flight goes horizontally 10 (or more) feet for every foot of descent. Its airspeed is tenfold less than the terminal velocity that would be expected for an object of that size and weight, and its vertical speed is at least a hundredfold less than terminal velocity.

If you reduce the amount of drag on the bomb, it will fall faster. If you reduce the amount of drag on the airframe, it will be able to descend slower.

Don't let anybody tell you the tail on an airplane works ``just like'' the feathers on an arrow.

6.1.1 Center of Mass Too Far Aft

Let's consider what happens to an airplane that has insufficient decalage. It is all too easy to create such a situation, by violating the aft limit of the airplane's weigh-and-balance envelope. Suppose you are hauling a bunch of husky skydivers. Suppose initially the loading is within the weight-and-balance envelope, but one by one all the jumpers wander to the very back of the cabin. As more and more weight accumulates in the back of the plane, the center of mass (center of gravity) moves aft, and you have to dial in more and more nose-down trim. The tail has to fly at a higher and higher angle of attack to support the added weight back there. Eventually you reach the point where the wing and the tail are flying at the same angle of attack — no decalage. At this point the airplane will not necessarily immediately fall out of the sky, but you'd better be careful.

The airplane will no longer have any angle of attack stability. It won't maintain its trimmed airspeed. (There are lots of things that could disturb the angle of attack, such as (a) an updraft, as depicted in figure 6.4, in analogy to the previous subsection, or (b) a speed change, which would cause a loss of lift — which in turn would cause an angle of attack change as discussed in section 5.2.) If you think you've got the airplane trimmed for 100 knots and 4^° angle of attack, it will be equally happy to fly at 200 knots and 1^° angle of attack, or 50 knots and stalling angle of attack!

Figure 6.4: Center of Mass Too Far Aft

In such a situation, you will need to keep very close watch on the angle of attack. You will need to constantly intervene to prevent the airspeed from wandering off to a dangerously high or dangerously low value — above V_NE or below V_S — leading to in-flight structural failure or a nasty stall. This is in marked contrast to a normal airplane with a normal amount of angle-of-attack stability which will maintain a definite angle of attack (and therefore a more-or-less constant airspeed) all by itself.

Not only is our aft-loaded airplane much more likely to stall than a normal airplane, the resulting stall will be the worst stall you've ever seen. In a normal stall, only the wing stalls; the tail keeps flying normally. The nose then drops, and the stall recovery begins automatically. Pushing on the yoke helps things along. But in our aft-loaded plane, notice that the tail is flying at just as high an angle of attack as the wing. It is perfectly possible that the tail will stall first. When this happens, the nose will pitch up! This guarantees the wings will stall shortly after the tail does. Now you've got an airplane with both the wing and the tailplane stalled. Pushing forward on the yoke will only make the tailplane more stalled. This is not a good situation.

At this point, the jumpers won't have to be asked twice to leave the plane. After they've left, you may be able to recover from the stall.

The stall is not the only thing you need to worry about with an aft-loaded airplane. You could just as easily get an airspeed excursion to a very high airspeed. That in turn could lead to structural failure.

The moral of the story: don't mess with the weight-and-balance envelope. The airplane's manufacturer did extensive analysis and testing so they could put the largest possible weight-and-balance envelope in the Pilot's Operating Handbook.

6.1.2 Center of Mass in the Middle

Now let's take another look at what happens when the center of mass is in the middle of the allowed envelope. Suppose you get another group of passengers (since the skydivers from the previous scenario are unwilling to fly with you anymore, and have taken up basket weaving instead).

Once again, suppose the center of mass starts out in the middle of the weight-and-balance envelope, as was depicted back in figure 6.3. Now suppose a few of the passengers move somewhat toward the front of the cabin. The center of mass will move forward. The tail will have less weight to support. If you don't do anything, the nose will drop and the airspeed will increase. Your first impulse will be to maintain altitude and airspeed by pulling back on the yoke. If the passengers promptly returned to their original positions, you would promptly be able to release the yoke pressure. But let's imagine that they stay forward. Rather than hold a steady back pressure on the yoke, you will dial in some nose-up trim to relieve the pressure.

As the center of mass moves farther and farther forward, you will need to dial in more and more nose-up trim to maintain the desired angle of attack. At some point the center of mass will move ahead of the center of lift of the main wing. The tail will then need to provide a negative amount of lift in order for the torques to be in balance, as shown in figure 6.5. There is nothing wrong with this; indeed most aircraft operate with negative tail lift most of the time.

Figure 6.5: Moderately Forward CM, Tail Download

The wing will have to generate enough lift to support the entire weight of the airplane, plus a little bit extra to overcome the downward force on the tail. (We have to have the forces in balance as well as the torques.) This in turn implies the wing will generate a little more induced drag, but the loss in performance is so small that you ordinarily won't notice it.

You will have lots and lots of decalage, so the airplane will have plenty of angle of attack stability. You can check this in the figure.

Some people are under the misimpression that the tail must fly at a negative angle of attack for the airplane to be stable. That's just not true. The real rule is just that the thing in back needs to fly at a lower angle of attack than the thing in front. If the angle is so much lower that it becomes negative, that is just fine, but it is not required.

The amount of stability you have depends on the angle of attack of the tail relative to the wing, not relative to zero.

6.1.3 Center of Mass, Lift, and Area

An amusing consequence of the decalage rule involves the center of area and center of lift of the airplane. To find the center of area non-mathematically, make a top-view picture of the airplane (on reasonably rigid paper). Cut away the background, leaving just the airplane itself, and see where it balances. The balance-point will be precisely the center of area.

The mathematical rule involved is a generalization of the rule you use to calculate the location of the center of mass. Various examples of the rule include:

To locate the center of mass: total up the product of mass times distance, summing over all elements of mass in the airplane. Divide by total mass; the result is the distance from the datum to the center of mass.
To locate the center of area: total up the product of area times distance, summing over all elements of area. Divide by total area; the result is the distance from the datum to the center of area.
To locate the center of lift: total up the product of lift times distance, summing over everything in the airplane that produces lift. Divide by total lift; the result is the distance from the datum to the center of lift.

All distances in these calculations are measured from some arbitrarily chosen reference point, called the datum. (The choice of datum doesn't matter, as long as you use the same datum for all measurements.)

6.1.4 Pitch-Axis Equilibrium

In steady flight the airplane must be in equilibrium. All torques must cancel, as discussed in section 19.7. There are various ways pitch-axis torques can arise; an extreme example is shown in figure 6.6. The engine is mounted high up on a pylon. (Seaplanes commonly do this.) In particular, the thrust is created some distance above where the drag is created. This means we have two forces and a lever arm — i.e. a torque.

Figure 6.6: Thrust Not Aligned With Drag Makes Torque

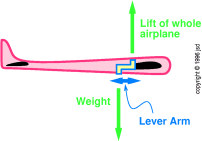Figure 6.7: Weight Not Aligned With Lift Makes Torque

The obvious way to cancel this torque is to have the center of lift (of the whole airplane) slightly offset from the center of mass (of the whole airplane). This causes a pitching moment — a torque around the pitch axis — as shown in figure 6.7.

The amount of torque produced by the thrust/drag misalignment will depend on the throttle setting. Specifically, when you open the throttle such a seaplane will tend to pitch down and accelerate; you will need to pull back on the yoke and/or dial in lots of nose-up trim to compensate. This is a rather undesirable handling characteristic. Airplane designers try to minimize the thrust/drag lever arm. Indeed, given a choice, it is better to put the thrust slightly below the drag, in which case opening the throttle causes the airplane to pitch up slightly and reduce its trim speed.

In all cases, the lift/weight lever arm (figure 6.7) is always very, very short compared to the thrust/drag lever arm (figure 6.6), since weight and lift are huge compared to thrust and drag.

There are other miscellaneous contributions to the pitch-axis torque budget. For one thing, any airfoil (even a barn door) produces a certain amount of torque — not just pure lift. The amount of torque grows with angle of attack, but some airfoils have the obnoxious property that the amount of torque is not strictly proportional to the amount of lift. Changing the airfoil (e.g. by extending flaps) changes the amount of torque.

The horizontal tail has a huge amount of leverage, and its coefficient of lift is adjustable over a very wide range. This means that by moving the yoke and/or trim, the pilot can move the center of lift (of the whole airplane) over a wide range. This in turn produces lots of torque to overcome the various nonidealities just mentioned.

I reiterate: the center of lift of the whole airplane is always very, very nearly aligned with the center of mass of the whole airplane. Otherwise the aircraft would not be in equilibrium.

On the other hand, because of the decalage rule, the center of area will always be behind the center of lift (and hence behind the center of mass). This is because the tail is ``loafing''. It is not doing its share of the lifting. The tail is a long way behind the center of mass, so it has a whole lot of leverage. It has a lot of area, out of proportion to the lift it is producing. This means the center of area will be aft of the center of lift.

To reiterate: the center of mass is significantly ahead of the center of area, not the center of lift.

Another misconception that is more nearly true is the notion that the center of mass of the whole airplane has to be ahead of the center of lift of the wing alone. This condition will occur if the tail is producing a negative amount of lift. As we have seen, this is possible, but not necessary.

Here's an explicit example. I've actually done the following experiment:

I took a Cessna 172 Skyhawk and put a couple of large pilots in the front seats, with no luggage and no other passengers. That meant the center of mass was right at the front of the envelope, so the tail had to produce considerable negative lift in order to maintain equilibrium. There was lots and lots of angle of attack stability.
I took the same Skyhawk and put a small pilot in the front seat, a large mad scientist in the back seat, and 120 pounds of luggage in the rear cargo area. That put the center of mass right at the rear of the envelope, so the tail had to produce considerable positive lift in order to maintain equilibrium. The airplane still had plenty of stability. (As far as the pilot could tell, it was just as stable as it ever was.)

The easiest way to determine whether the tail lift is positive or negative is to observe the direction of motion of the tip vortices. This can be done using yarn contraptions that dangle from the tips of the horizontal tail.

6.1.5 Canards Operate on the Same Principle

Some airplanes have the main wing in the back. They get their stability from a much smaller wing (called a canard) in the front. Anybody who believes that ``the thing in back always has to fly at a negative angle of attack'' will have a hard time understanding how this works. The thing in back is the main wing! It had better be flying at a normal, positive angle of attack.

In fact, you can build a whole sequence of planes, gradually transforming a canard configuration into a normal configuration by making the rear wing smaller and the forward wing larger. If you do it right, all of them will have positive lift from the tail, and all of them will be stable — all for the same reason.

According to the decalage rule, the thing in front must be flying at a higher angle of attack. The canard configuration is analyzed in figure 6.8.

Figure 6.8: Canards Operate on the Same Principle

In the top panel, the airplane is buzzing along in still air. The main wing (in the back) is operating at a normal cruise angle of attack, 4^°. The canard is operating at 10^° angle of attack. This gives us 6^° of decalage, which should be plenty. All the forces and torques are in balance.

Then, as shown in the lower panel, the airplane flies into an updraft. The updraft affects the canard and the main wing equally, increasing both angles of attack by one degree. This represents a 25% change for the main wing, but it represents only a 10% change for the canard. The airplane will pitch nose-down, as it should. The system will return to equilibrium only when it returns to the original (trimmed) angle of attack.

In a canard-type airplane, the center of mass is clearly always ahead of the main wing, but this is not what creates stability. The center of mass has to be ahead of the center of area (including the area of the canard). The only way this can happen is if the canard produces a huge amount of lift, out of proportion to its area. The next time you see such an aircraft parked on the ramp, take a look. You will see that the canard is installed at a tremendously large angle of incidence.⁶

Since the canard must fly at a higher angle of attack than the main wing, stalling of the canard is always a concern during maneuvers that involve a high angle of attack — e.g. landing. This explains why canard airplanes tend to have high landing speeds (which in turn requires rather long runways) — to land at a nice slow speed you have to fly the main wing at the highest possible coefficient of lift. Now for stability the canard has to fly at an even higher coefficient than that, which calls for some compromises and/or some very tricky designs.

6.1.6 Beyond Decalage

Decalage is the main issue but not the only issue affecting the airplane's angle of attack stability. The following points are mentioned only briefly, because they are of more interest to airplane designers than to pilots.

In maneuvers where the airplane is rotating around its pitch axis, pitch damping must be taken into account, as discussed in section 6.1.8.
The tail flies in the propwash (to a greater extent than the wing). This reduces stability, because it reduces the steepness of the tail's lift versus angle of attack curve. Remember that stability depends on the torque due to the tail increasing more steeply than the torque due to the forward wing when an overall angle of attack change occurs. Alas, the propwash hits the tail at the same angle regardless of what the relative wind is doing, so stability is reduced.
The tail flies in the downwash of the wings. This reduces stability, again because it reduces the steepness of the tail's lift versus angle of attack curve. The air flowing off the back of the wing tends to flow straight off the trailing edge, regardless of the angle at which it approached the wing. Also, when the airplane's overall angle of attack changes, the aft wing can move in or out of the forward wing's wake. This changes the lift curve of the stabilizer in ways that are hard for designers to predict. Further, any change in the downwash pattern can move the angle of attack to a new equilibrium point. Therefore, on most aircraft, extending the flaps perturbs the trim speed, as discussed in section 5.5.
In a steep turn, the trimmed angle of attack will decrease slightly, because rotations are not commutative, as discussed in section 19.6.5.
A propeller disk in front of the airplane reduces stability, because of the way the airflow through the disk changes with angle of attack. (Pusher props increase stability.)
A cambered wing reduces stability. Conversely, you can make an airfoil that doesn't need a tail to be stable, if you give it enough reverse camber; flying-wing aircraft use this trick.
The aspect ratio of an airfoil affects the steepness of its lift versus angle of attack curve. You get more stability if you have a short fat wing and a long skinny tail.
Sweepback affects the lift versus angle of attack curve.
Ground effect changes everything. This is important because you want the airplane to be well behaved during takeoff and landing, not just during cruise.
As discussed in section 6.1.7, designers can use springs and/or bobweights to pull the airplane slightly away from its purely aerodynamic trim point.

To reiterate: decalage is the primary means for creating angle of attack stability. The other effects mentioned in this subsection determine how much decalage will be needed.

6.1.7 Springs and Bobweights

In addition to the purely aerodynamic contributions discussed at the beginning of section 6.1, some airplanes have non-aerodynamic contributions. Imagine an aircraft that is not quite in trim from a purely aerodynamic point of view, so that you must apply pressure to the yoke. Now imagine that you relieve this pressure using a spring connected to the yoke. The airplane is now in trim in an overall sense. It is trimmed approximately, but alas not exactly, for a definite angle of attack. This is because at a higher airspeed, the aerodynamic force on the yoke is larger. This force overpowers the spring, changing the angle of attack.

Designers can also use weights (called bobweights) to pull the airplane slightly off its aerodynamics trim point. That makes the angle of attack depend on load factor as well as airspeed. Designers generally try to design an airplane to use aerodynamic trim alone, but sometimes adding springs and/or bobweights are the expedient way to create an acceptable ``control feel''.

6.1.8 Pitch Damping

Let's consider what happens during a maneuver where the aircraft is rotating around the pitch axis. This includes loops, phugoids (as discussed in section 6.1.12), and steep turns. Note that for any bank angle steeper than 45 degrees, a turn involves more pitch-axis rotation than yaw-axis rotation.

Figure 6.9: Pitch Damping

Figure 6.9 shows what the relative wind does during an upward-pitching maneuver. The angle of attack of the tail is increased relative to the angle of attack of the wing. The aerodynamic effect is similar to the effect you would get by applying some nose-down trim. That is, the airplane wants to fly at a lower angle of attack than it would in the corresponding situation without the pitching motion. This effect is the main contribution to pitch damping. It is helpful because it makes phugoid oscillations die out after a few cycles. On the other hand, it makes graveyard spirals slightly more dangerous.

6.1.9 Center of Mass Too Far Forward

Let's finish our discussion of the pitch axis torque budget by considering what happens if the center of mass is too far forward. The airplane in figure 6.10 has too much weight in the forward cargo area. In order for the torques to be in balance, the tail must be flying at a tremendous negative angle of attack.

Figure 6.10: Center of Mass Too Far Forward

Stability is not the problem here. The aircraft has vast amounts of decalage and will be exceedingly stable. If the situation is not too extreme, the aircraft will be flyable until the time comes to raise the nose for the landing flare. When you pull back on the yoke, the tail will stall. This is the mirror image of the usual stall: the tail stalls because its angle of attack becomes too negative. The more stalled it gets, the less (negative) lift it produces. The nose of the airplane will snap down like a mousetrap.

This can definitely happen any time you exceed the forward limit of the weight-and-balance envelope; please don't get the idea that you are OK unless you actually put anvils in the forward baggage locker.

Some aircraft have very tight restrictions on the center of mass. Beechcraft Sundowners and V-tailed Bonanzas are notable examples; a Sundowner with just two pilots and full fuel is well beyond the forward limit of the center-of-mass envelope. The correct solution to this problem is to use ballast. For the Sundowner, 50 pounds of ballast at the back of the luggage compartment typically suffices.

I once knew some people who liked to fly a Sundowner but didn't like to bother with the ballast; they complained that the airplane was tricky to handle in the flare and they wondered why it had to go into the shop for nose gear repairs three times in a six-month period. The airplane was destroyed in a crash so they don't have this problem anymore.

Ballast may seem low-tech, but it does the job. I recommend using jugs of water as your ballast. That way if you need ballast on the outbound leg but need full load-carrying capacity on the return leg (satisfying the balance requirement with cargo and rear-seat passengers) you can dump out the water and keep the jugs; with other forms of ballast you'd need to worry about how to replace or retrieve it.

Here's a dirty trick that might save your neck in an emergency. If you need to land an airplane that is too nose-heavy, use soft-field technique. That is, carry some engine power during the flare. The propwash over the tail will give you a little more control authority and delay the tailplane stall. On the other hand, if you are smart enough to anticipate this situation, you ought to be smart enough to load the airplane properly so that the situation doesn't arise.

6.1.10 Other Failure Modes

There are lots of ways to violate the weight-and-balance envelope. As discussed above,

If the center of mass is too far aft, the airplane will lose its angle of attack stability. The airplane will not maintain its trimmed airspeed.
If the center of mass is too far forward, you run the risk of a negative-alpha tail stall.

Additional things that you need to worry about include:

Compliance with your airplane's official weight-and-balance limits is required by FAR 91.9(a). The regulators take violations pretty seriously, as indeed they should.
There is always a limit to how far you can deflect the yoke. You may run out of control travel before you reach the stall or the zero-stability point. This is not entirely good news, because it means you lose control of the pitch axis sooner than you otherwise would.
Of course, if you put too many anvils in the baggage compartment you need to worry about structural failure of the compartment floor — in addition to whatever stability and control problems you have.
As the center of mass moves forward, the phugoid oscillations (as discussed in the section 6.1.12) tend to become more pronounced.
Et cetera, et cetera.

6.1.11 Practical Considerations

Airline crews are required to check the weight and balance in detail for every flight. In practice, general aviation pilots often pre-calculate typical cases. For instance, I know that in one of the planes I commonly fly, two pilots (of any reasonable size) and full fuel is well within the envelope, so I know I don't need to check the details.

If I am flying an unfamiliar airplane, or an unusual mission (e.g. taking three linebackers as passengers in a Skyhawk) then I will check the weight and balance very carefully.

I have a computer program that makes it quick and easy.

6.1.12 Phugoid Oscillations

As we have seen, it is a good thing for the airplane to have plenty of stability of angle of attack, and this is relatively easy to arrange.

In fact, the airplane's desire to return to its trimmed angle of attack is so strong that it generally returns too quickly, and overshoots. To say it in slightly more technical terms, airplanes essentially never have as much damping of the pitch axis as you would like.

You can do the experiment yourself easily enough: Trim the airplane for straight and level flight at some reasonable airspeed. Pull back on the yoke until the airplane slows down about ten knots, and then let go. The airplane will not just return to its trimmed condition (pitch attitude, airspeed, and angle of attack) but will pitch down and speed up too much. Of course, the airplane will shortly discover this, and will pitch up and slow down again — but will overshoot in the other direction. This is shown in figure 6.11. This phenomenon is called phugoid oscillations (pronounced fyoo'goid). After a few cycles, the oscillations will die out⁷ and the airplane will return to the previous trimmed condition.

Figure 6.11: Phugoid Oscillations

As the center of mass moves forward, you get more and more stability, but less and less damping of the pitch axis — therefore worse phugoids.

Fortunately, the phugoid oscillation is so slow that you can easily arrest the oscillation. If at point (1) in the figure you push the nose down to level pitch attitude, the airplane will be on altitude, on airspeed, and level — and the phugoid will be over. Similarly, if at point (3) you pull the nose up to level pitch attitude, the phugoid will be over instantly. If starting at point (2) you hold level pitch attitude, the airplane will take a while to accelerate to its trim speed; you will need to maintain back pressure on the yoke until it does. Similarly, starting at point (4) you can push on the yoke until the airplane decelerates to its trim speed.

You may find this recovery procedure counterintuitive at first, so it's good to practice it a few times. See also section 10.6.2 for a general discussion of how to recognize oscillations and how to respond.

You can expect a phugoid whenever the airplane's airspeed or pitch attitude is disturbed from the trimmed equilibrium condition. Rough handling of the controls will do it for sure. Even if you leave the controls alone, a series of updrafts and downdrafts can easily initiate a phugoid (if you are not paying enough attention to the pitch attitude). This will result in much larger altitude and airspeed excursions than would have occurred if level pitch attitude had been maintained.

On July 19, 1989, the #2 engine of a DC-10 disintegrated, disabling the hydraulic systems that operate the flippers.⁸ The pilots managed to fly the beast to the Sioux City airport, controlling it with just the #1 and #3 throttles — the only controls still available. Every power change provoked a few cycles of phugoid oscillation. The pilots had never been taught about phugoids; they had to figure it out on the fly (so to speak). The captain of this flight, Al Haynes, has given a number of lectures recounting the experience. A videotape exists, too — highly recommended.

If you think the word ``phugoid'' looks strange, you're right. The origins of the word are highly amusing. Apparently Lanchester (who was the first to analyze these oscillations) wanted to coin a fancy name, based on Greek roots. He started with the English word ``flight'', which is, unfortunately, a homonym. From there, he stumbled onto the Greek word for fleeing instead of flying. The same root ``fugh'' has come down to us in the words ``fugitive'' and ``centrifuge''. So a term that was meant to translate as ``aeronautical oscillation'' actually comes out as ``fugitive oscillation''. Oh well.

6.2 Spiral Dive

6.2.1 Which Way Is Up?

People think they know which way is up, but they don't. The semicircular canals in your inner ear will tell you which way is up for a few seconds, but after that, you don't know. Not without looking.

If you can see the horizon, that tells you which way is up. If you can see the ground below you, that tells you which way you are turning. If you have a horizon gyro and a rate-of-turn gyro, and you are skilled at interpreting them, that's fine. But suppose you are flying in clouds, or over an unlighted area on a dark, overcast evening. If you look away from the instruments, you have no idea which way is up, or which way you are turning.

Sooner or later you will get into a bank, and then the bank angle will increase rather rapidly (due to the overbanking tendency, section 9.4).

6.2.2 Overview

The result is called a spiral dive. It has a well-deserved nickname: graveyard spiral. Except for running into something, a spiral dive is almost the only way you can inadvertently destroy an airplane.⁹

This will be a good application and illustration of what we have just learned about angle of attack stability. This subsection gives a quick overview of the situation; a more detailed discussion is presented in subsection 6.2.3.

Figure 6.12: Forces in a Steep Turn

Imagine that you are initially trimmed for straight and level flight at, say, 100 knots. Then you inadvertently enter a steeply banked turn. Figure 6.12 shows the forces acting on the plane in level flight and in the turn. Let's imagine that the plane weighs exactly one ton. In level flight the downward force of gravity is exactly canceled by the lift produced by the wings, so the wings must be producing one ton of lift.

In the turn, though, the wings must produce enough force not only to support the weight of the airplane (vertically), but also to change the airplane's direction of motion (horizontally). The total force can be quite large: In a 60^° turn, two tons of force is required. In a 75^° turn, almost four tons of force is required, as shown in figure 6.13.

Figure 6.13: Forces in a Very Steep Turn

In order to produce 4 tons of lift, the airplane must fly at roughly 200 knots — twice the wings-level trim speed.

Now let's imagine that after spiralling for a while, you discover what is going on. The first thing you should do is to roll back to wings-level attitude. That solves your most urgent problem, but does not get you completely out of danger.

So let's think about the new situation. The airplane is still going roughly 200 knots. (It is going to slow down, but it hasn't yet done so.) It is still trimmed for cruise angle of attack. Therefore, the wings are still producing 4 tons of lift. You've got a real problem. Previously, you had 4 tons of lift pointing mostly horizontally, pulling you around the turn. Now you've got 4 tons of lift, pointed vertically — pulling you into a loop! This situation is illustrated in figure 6.14.

Figure 6.14: Rolling Out of a Spiral Dive

Note that a properly-executed aerobatic loop-de-loop involves only 4 Gs of force at the bottom. There is no doubt that an airplane rolling out of a 75^°-banked spiral has enough energy to flip right over onto its back — unless you do something. This is the phugoid from hell.

Therefore, when rolling out of a steeply-banked turn, plan on pushing on the yoke, to prevent a dangerously nose-high attitude.

6.2.3 General Discussion

Spiral dives are really important. Now that we've learned the ``lay of the land'', let's go through the scenario again in a little more detail.

The first step in the scenario is to have one wing down. There are lots of ways this could happen. If the airplane is not in good lateral trim (perhaps because you've burned more fuel from one tank than another, or because the passengers and cargo are not symmetrically distributed) one wing might drop as soon as you let go of the controls. Even if the trim is perfect, turbulence certainly can make one wing go down.

Having a wing down produces a whole series of consequences.¹⁰ The earliest step in this series is shown in figure 6.15. The airplane has just entered a bank. The airspeed is the same as it was before the bank began, simply because it has not yet had time to change.

Figure 6.15: Earliest Consequence of Bank

We see that the vertical component of lift is insufficient to balance the weight of the airplane. (Compare this figure with figure 6.12 or figure 6.13.) The unbalanced force will cause the airplane to drop straight down. This is the same as the ``albatross effect'' discussed in section 5.2 . Then, as soon as any appreciable downward velocity develops, the airplane will pitch down and speed up — because the airplane wants to maintain its trimmed angle of attack¹¹ as discussed in section 6.1.

The combined effect of vertical damping and angle of attack stability will cause the airplane to speed up until the lift vector is long enough that its vertical component balances the weight of the airplane, as depicted in figure 6.12. The load factor is defined to be the ratio of the lift the wing is actually producing, relative to the lift required for unaccelerated flight.

To say it yet another way, the load factor specifies how many G you pull in a steady turn. It grows explosively at large bank angles, as shown in figure 6.16.

Figure 6.16: Load Factor versus Bank Angle

The trim speed increases almost as dramatically, as shown in figure 6.17. In a 60^° bank, the airplane will want to maintain a speed that is roughly 141% of its wings-level trim speed. In a 75^° bank, the trim speed is roughly 200% of the wings-level trim speed. In every airplane I know of, if you start out at cruise and then double the airspeed, you will be well beyond V_NE (never-exceed airspeed). This creates the risk of immediate structural failure, especially if you do something foolish like pull back on the yoke.

Figure 6.17: Trim Speed versus Bank Angle

The trim speed grows in proportion to the square root of the load factor. There is a simple reason for this. Recall (from e.g. section 4.4) the key formula:

lift = ½ rV² × coefficient of lift × wing area (6.1)

When you enter a spiral dive, the wing area of the airplane doesn't change, the density of the air (r) doesn't change, and the coefficient of lift¹² doesn't change much, either.

Consider the following scenario: imagine you are not proficient at instrument flying, but you find yourself flying through clouds or flying on a dark night over the desert. You will very soon lose track of which way is up.

At some point you perceive that something is wrong, because you are being pushed into your seat by unusual G loads. Four Gs will definitely get your attention. You should also be able to hear the unusual wind noises, as the airplane accelerates to roughly 200% of its normal cruise speed. You will not have any sensation that you are turning. Even if you suspect you are in a turn, you will not be able to tell which direction you are turning, without referring to outside references or gyroscopic instruments.

Because of the overbanking tendency, the bank angle will continue to increase. The airspeed, descent rate, and load factor will increase accordingly. There will be no significant slip angle.

6.2.4 Recovering From a Spiral Dive

If you find yourself in an unusual turning, descending situation, the first thing to do is decide whether you are in a spiral dive or in a spin. In a spiral dive, the airspeed will be high and increasing; in a spin the airspeed will be low. Also, the rate of rotation in a spiral is much less; the high speed means the airplane has lots of momentum and can't turn on a dime.

Here is the correct procedure for recovering from a spiral dive .¹³

Smoothly roll the wings level.
Simultaneously use your other hand to retard the throttle. This is not an essential step, but it might prevent the engine RPM from going beyond redline.
Do not pull on the yoke at all. When you finish rolling out of the turn, the airplane will have 15 degrees or so of nose down pitch attitude, but it will immediately pitch up all by itself, at the rate of roughly 15 degrees per second. You should just wait a second or so until the airplane returns to level flight attitude, and then push on the yoke to maintain a reasonable attitude.
As the airspeed returns to normal, the amount of pushing you need goes to zero. You can re-open the throttle and fly away.

If you have good outside references, by all means use them to re-establish wings-level attitude and then to re-establish a reasonable pitch attitude.

If you don't have good outside references, you should not rely on the attitude indicator (artificial horizon). The attitude indicator contains a gyro mounted on ordinary mortal gimbals, which can only accommodate a limited range of pitch and bank angles. A steep spiral can easily cause the gyro to tumble, whereupon it will need several minutes of relatively straight and level flying before it can re-erect itself. Military aircraft have non-tumbling attitude indicators, but you're not likely to find such things in a rented Skyhawk. Therefore, you should roll the wings level by reference to the rate-of-turn gyro.¹⁴ Being a rate gyro (as opposed to a free gyro) it has no gimbals, and therefore can't possibly suffer from gimbal lock.

Remember: to recover from an unusual attitude, use the rate-of-turn gyro to level the wings.¹⁵ This is a good example of the sort of information you have to get from books. Presumably during training you will never do anything bad enough to tumble the attitude indicator.

Controlling the pitch attitude without relying on the artificial horizon requires thoughtful use of the airspeed indicator. At the point where the wings have just been returned to level, the airspeed will be something like twice what it ought to be. It will decrease slowly at first, then faster and faster. Your job is to keep the airspeed from unwinding too quickly. Pick some rate like 5 knots per second, and push on the yoke enough to keep the airspeed needle from moving faster than that.

Don't worry that pushing on the yoke will cause the airplane to fly into the ground. The airplane will climb and it will pitch up all by itself; your job is to keep it from pitching up too much. Remember¹⁶ the law of the roller coaster: 9 feet per knot, per hundred knots (section 1.2.1). As you slow down from the high-speed dive, most of that airspeed energy will be converted back to altitude. Wait until the airspeed returns to a reasonable value before you worry about returning to your exact intended altitude.

You can also use the altimeter to help manage the pitch attitude. As soon as the altimeter needle starts moving upward, you should push on the yoke to keep the needle from moving too quickly.

Unless you know you are proficient on instruments, you should not rely too heavily on the vertical speed indicator. It has weird built-in delays that can be hard to interpret.

Very, very few pilots have been taught how to handle a spiral dive correctly. In fact, the official FAA Flight Training Handbook (reference 21) currently¹⁷ says not once but four times (on pages 65, 187, and 188) that the procedure for recovering from a spiral dive calls for pulling back on the yoke. It says that you shouldn't pull back too much, but nowhere does it say that you might need to push forward. The FAA Instrument Flying Handbook also discusses spiral dives without giving the slightest hint that forward pressure might be necessary. The vast majority of other pilot training books suggest the same wrong procedure.

In some aircraft, including many trainers, retarding the throttle produces a nose-down pitch change which helps with the recovery, just like a small push on the yoke. Although this helps, it is definitely not sufficient in all cases. What's worse, there are some aircraft (as mentioned in section 6.1.4) in which retarding the throttle produces a nose-up pitch change.

In a not-very-steep spiral, it hardly matters what recovery procedure you use, but the more serious the spiral, the more crucial it is to use the correct procedure.

Let's look again at what happens if you use the wrong procedure. You are buzzing along in the clouds, and you get into a spiral dive. You smoothly roll the wings level (so far so good). The next thing you know the plane pitches up into a ridiculous nose-high attitude. If we are talking about a really high-speed spiral dive, the airplane will loop right over on its back. If the spiral was more moderate, you will ``only'' do a tail slide or hammerhead or something.

This is just about the last thing you need. You were in a spiral dive, which was bad enough — but now you are in some horrendous unusual attitude, stalled and/or upside down, still in the clouds.

If you use the correct procedure, recovering from the spiral dive is straightforward. If you use the wrong procedure, the ensuing unusual attitude could be very hard to recover from.

If you use the widely-taught ``standard'' procedure and pull back on the yoke, it can only make things worse. Pulling back will increase the angle of attack, and therefore the coefficient of lift. This might make things much worse, for several reasons:

It will make you more likely to wind up in an unusual attitude.
Since the wings were already developing 4 Gs, you don't need to increase that very much before you snap the wing spar.
Even if you don't break the airplane, you might break the pilot. It varies a lot from person to person, but 6 Gs, especially suddenly and unexpectedly, is enough to drain the blood from your head and collapse some of the blood vessels in your brain. Even if the G load is removed, it will take a while for you to regain consciousness. Furthermore, even after you regain consciousness you will not be as smart as you used to be. Your thought processes will be severely impaired for a couple of minutes if not longer. Since you were already in an emergency situation before you blacked out, this is really the last thing you need.

The correct recovery procedure is rather counter-intuitive. Because the airplane is descending and because it is going too fast, your instincts will tempt you to raise the nose. The problem is that the airplane's instincts tell it to do the same thing — and it will pitch up too much unless you intervene.

6.2.5 Try It Yourself

You don't need to take my word for what happens — you can go out and do some experiments yourself. You probably want to take an instructor along, but it is not absolutely necessary if you are careful. Experiment with shallow banks before messing with really steep banks.

Start by trimming the airplane for level flight at a low-cruise airspeed, say 100 knots, and clearing the area. Roll the airplane into a 45^° bank and let it descend and accelerate. Leave the throttle alone, leave the trim alone, and don't push or pull on the yoke. Apply enough aileron to keep the bank from getting steeper than 45^°. Wait a few seconds for the airspeed and descent rate to stabilize, then roll the wings level and watch what happens.

After you know what happens in a 45^° bank, try it again at 50^°, and work your way up to 55^°. Don't even think about exceeding 60^° without having an aerobatic-qualified instructor on board. The margin between an ``interesting'' spiral and a genuine emergency becomes small, as you can see in figure 6.16.

When you roll out of the 55^° or 60^° banked spiral, the nose will be pointed about 15 degrees below the horizon. If you count off one second, the pitch attitude will be level. After two seconds, it will be 15 degrees nose up. After three seconds, it will be 30 degrees nose up, which is an awful lot. You will be quite happy to grab the controls at that point and push the aircraft back to a reasonable pitch attitude.

Repeating the experiment under the hood is also edificational.

Normally when you demonstrate a steep turn, the airspeed does not increase — in fact it decreases. That is because you retrim and/or pull back on the yoke, causing the angle of attack to increase. In contrast, our explanation of the spiral dive assumed that it was an inadvertent spiral dive, so the angle of attack stays nearly the same and may even decrease¹⁸ slightly. One thing is certain: the wings have to create enough lift to support the effective weight of the airplane (real weight times load factor). If the coefficient of lift stays the same, the speed has to increase; if the speed stays the same, the coefficient of lift has to increase.

6.3 Summary

The airplane has considerable angle of attack stability. The airplane is trimmed for a definite angle of attack.
Speaking of pitch stability is less accurate than speaking of angle of attack stability.
The biggest contribution to angle of attack stability is decalage. The thing in back flies at a lower angle of attack than the thing in front. The thing in back may, but need not, fly at a negative angle of attack. A canard obviously requires the thing in back (the main wing!) to have positive angle of attack.

Angle of attack stability is reduced as the center of mass moves aft.
The trim wheel is used to choose what the trimmed angle of attack will be. The yoke is a convenient extension of the trim wheel, for temporary changes in angle of attack.
The trimmed angle of attack corresponds to a definite airspeed (assuming constant load).
Configuration changes (flap extension, power changes etc.) have side-effects on the trim speed.
In a turn, the load factor increases. In order to maintain its trimmed angle of attack, the airplane pitches down and speeds up. In a steep turn (assuming you don't change the angle of attack using the yoke and/or trim), the speed-up is substantial.
When you roll out of a steep turn, the airplane tends to pitch up all by itself. You may need to push on the yoke to maintain control.

1: For a general discussion of the concepts of force, torque, and moment, see section 19.7.
2: For a general discussion of the principles and terminology of equilibrium stability, and damping, see chapter 10.
3: We find it convenient to use the center of mass of the airplane as our pivot point, measuring all lever-arms from that point, so the force of gravity contributes nothing to the pitch-axis torque calculations. Of course, the answers come out the same no matter what pivot is chosen. See also section 6.1.4 for a discussion of sundry additional pitching moments.
4: ...rhymes with ``day-garage'', with the accent on the last syllable.
5: The word can equally well refer to a difference in angle of attack between the two wings of a biplane.
6: One famous exception: the Wright brothers' original airplane (``Flyer I'') on display in the Smithsonian does not have enough decalage to produce positive angle of attack stability. It must have required a goodly amount of skill and constant attention during flight.
7: See section 6.1.8 for a discussion of why it dies out.
8: ... not to mention the ailerons, rudder, flaps, et cetera.
9: Other disasters such as in-flight fires are vanishingly improbable by comparison.
10: Among other things, airplane will turn, pitch down, speed up, and experience a load of more than one G. Also, once the airplane is substantially banked (more than 30 or 40 degrees) the overbanking tendency will cause the bank to get steeper and steeper.
11: The angle of attack remains constant to a good approximation, but because of the pitch damping discussed in section 6.1.8 and other nonidealities discussed in section 6.1.6, it won't be exactly constant.
12: Remember, coefficient of lift is determined by angle of attack — and the airplane is trimmed for definite angle of attack. We are assuming an inadvertent spiral dive, so you presumably haven't changed the angle of attack by pushing or pulling on the yoke, or by messing with the trim.
13: Recovery from a spin is discussed in section 18.7.
14: That is, the turn needle or turn coordinator, whichever you happen to have.
15: When the wings are level, you will observe zero rate of turn on the rate gyro. Remember that this instrument indicates rate of turn, not bank angle per se.
16: See section 1.2.1.
17: Mid-1997. The FAA is working on a revision of the Flight Training Handbook. Let's hope these sections are the first to be changed.
18: ... due to pitch damping, as discussed in section 6.1.8.

[Previous] [Contents] [Next]
[Comments or questions]