[Previous] [Contents] [Next]
[Comments or questions]

10 Equilibrium, Stability, and Damping

Three of the most useless things in aviation are:

The airspace above you.
The fuel not on board.
The runway not in front of the wheels.

Several parts of this book make use of the concepts of equilibrium, stability, and damping. This section defines the concepts a little more precisely and clarifies the relationships between them.

10.1 Equilibrium

The word equilibrium is quite ancient. The word has the same stem as the name of the constellation ``Libra'' — the scale. The type of scale in question is the two-pan balance shown in figure 10.1, which has been in use for at least 7000 years. The compound word ``equilibrium'' translates literally as ``equal balance'' and means just that: everything in balance, no unbalanced forces.

Figure 10.1: Equilibrium — Forces in Balance

The wheel is more modern than the balance; it has been in use for ``only'' some 5500 years. It provides some more sophisticated illustrations of equilibrium and related concepts. If we make the wheel lopsided by attaching a weight to the rim at one point, the system will be out of equilibrium unless the weight is exactly at the top or bottom. If we prepare the system in an unbalanced state and then let go, it will immediately start rotating.

Figure 10.2: Equilibrium and Stability

To reiterate, and as indicated in figure 10.2, there are three ways to make the wheel be in equilibrium: (1) position the weight at the bottom, (2) remove the weight entirely, or (3) position the weight at the top.

10.2 Stability

Stability has to do with how the system responds if we move it a little ways from its equilibrium position. There are three possibilities:

Positive stability means that if the system is displaced a little ways from its equilibrium position, it will generate a force tending to push it back towards equilibrium. The wheel with the weight positioned at the bottom is an example of positive stability.
Neutral stability (also called zero stability) means that if the system was in equilibrium and you displace it slightly, it remains in equilibrium. No force is generated. The perfectly balanced wheel is an example of this.
Negative stability means that if the system is displaced a little ways from its equilibrium position, it will generate a force that tends to push it farther from equilibrium. The wheel with the weight at the top is an example of negative stability.

It usually doesn't make much sense to talk about stability except for systems that are in equilibrium or nearly so.

For a multi-dimensional system, we get to ask about the stability of each axis separately. For example, consider an egg resting on a horizontal table. An ideal egg has zero stability against motion in one direction: it is free to roll around its axis of symmetry. On the other hand, it has positive stability against motion in the end-over-end direction; if you rock the egg slightly by pushing its nose down, it will tend to return to its original state.

10.3 Damping

A system exhibits damping if motion of the system produces a force that opposes the motion.

A bicycle wheel provides a good demonstration of a system with very little damping. Assuming the bearings are good and the wheel is not touching anything, when you spin the wheel it will keep going for more than a minute. Air friction produces very small forces that eventually cause the wheel to slow down.

A bicycle wheel that is rubbing against something is much more heavily damped. When it is in motion, rubbing friction can create large forces that oppose the motion and bring the motion to a stop.

A dynamical system can exhibit negative amounts of damping, but this is harder to demonstrate with a simple system. Negative damping tends to make the motion increase, which means that energy is being added to the system from somewhere; therefore simple friction can never produce negative damping.

Nose wheel shimmy of an airplane is a good example of what happens if a system has a negative amount of damping. If the aircraft is moving along the ground at high speed, the nosewheel will eventually hit a pebble or something. The nosewheel is then no longer aligned with the direction of travel. By the usual ``castering'' principle, this causes a force that tends to return the wheel to its proper position (that is, the wheel exhibits positive stability). Unfortunately, many aircraft have too much stability, and too much inertia in the castering mechanism. The result is that the wheel tends to overshoot its equilibrium position and continue to the other side, going out of alignment in the opposite direction by an even greater amount. The result is an oscillation that quickly grows to large amplitude.

Note the relationship of stability and damping: when the wheel is being forced back toward alignment, the force is toward the equilibrium position (positive stability) but is in the same direction as the motion (negative damping).

To eliminate the shimmy problem, a hydraulic ``shimmy damper'' is installed on the nose wheel. Figure 10.3 is cutaway drawing showing how a hydraulic damper works. It consists of an oil-filled cylinder, plus a pushrod attached to a disk inside the cylinder. When the pushrod moves from side to side, oil is forced to flow through the small holes in the disk. This creates a force proportional to the velocity of motion — i.e. damping.

Figure 10.3: Hydraulic Damper

Sometimes the fluid leaks out of the damper, and even more commonly the linkages connecting the damper to the wheel become worn and loose. This makes the damper ineffective, whereupon the you get a vivid demonstration of negative damping. A preflight check of the damper and linkages is easy and worthwhile.

Also... as discussed in chapter 5, the airplane's rolling motion and pure vertical motion are normally very heavily damped, but this damping goes to zero and becomes negative at the stall.

10.4 Relationship of Stability and Damping

To reiterate: stability refers to a force that arises depending on the position of the system; damping refers to a force that arises depending on the velocity.

In old-fashioned terminology, what we call ``stability'' was sometimes called ``static stability'', and what we call ``damping'' was sometimes called ``dynamic stability''. What's worse, occasionally both terms were shortened to the single word, ``stability'', which was unnecessarily confusing.

Also, modern usage prefers ``damping'' not ``dampening'' — if you start talking about a ``dampener'' people will think you want to moisten the system.

Stability can be positive, zero, or negative; damping can also be positive, zero, or negative. A dynamical system can display any combination of these two properties — nine possibilities in all, as shown in figure 10.4. In the top row, the bicycle wheel is dipped in molasses, which provides damping. In the middle row, there is no damping. In the bottom row, you can imagine there is some hypothetical ``anti-molasses'' that provides negative damping.

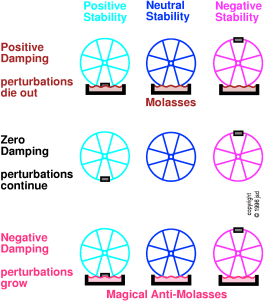Figure 10.4: Stability and Damping — Possible Combinations

10.5 Oleo-Pneumatic Struts

A great example of a device that provides a force that depends on position and a force that depends on velocity is the oleo-pneumatic strut, which is widely used on landing gear as a combination spring and shock absorber. It consists of a piston in a cylinder filled with both oil (``oleo'') and air (``pneuma''), as shown in figure 10.5. If the piston is moved up into the cylinder, the air at the top of the cylinder is compressed. (The hydraulic oil is essentially incompressible.) This ``air spring'' creates a force that depends on the position. As the piston moves, the oil in the hollow part of the piston is forced to flow through the holes in the disk, creating a force that depends on the speed of motion, using the same principle as the damper discussed previously.

Figure 10.5: Oleo-Pneumatic Strut

It is important that the strut contain the right amount of air and the right amount of oil. Problems can arise more easily than you might think.

Suppose that over time, some of the oil leaks out of the strut on your airplane.¹ Your friend, Murgatroyd Fudpucker, borrows the plane and notices during preflight that one of the struts is low — that is, not enough of the piston is protruding from the cylinder. Murgatroyd gets out a bicycle pump and adds air to the strut. Everything now looks fine. During future preflight checks, a passive glance the strut will give you the impression that everything is OK.

Alas, things are not OK. The problem is that oil has been replaced with air. Since air is a thousand times more compressible than hydraulic oil, the amount of force it takes to make the strut ``bottom out'' has been greatly reduced. If you or Murgatroyd makes even a slightly hard landing, the piston will smash against the end of the cylinder, metal to metal. This has roughly the same effect on the airframe as hitting it with a sledgehammer. Repairs could be very, very expensive.

Therefore, if there is any chance that the airplane has been mis-serviced since the last time you flew it, you should check not only the height of the struts, but also their springiness. To check a main-gear strut, lift up the wing a few inches and then let it drop. Similarly, to check the nose strut, lift up the nose (perhaps by pushing down on the tail) a little ways and then let it drop. If any strut compresses more than it should (e.g. if it comes anywhere close to bottoming out), do not fly the airplane until the strut has been properly serviced with air and oil.

There is a thin coating of oil on exposed part of the piston, which collects dust. When the piston is shoved into the cylinder, the O-ring will scrub the dirt down the piston and cause it to collect in a ring called the scrub line. Observing the scrub line can tell you how close the strut has come to bottoming out recently.

Please do not get the impression from the foregoing discussion that ``air is bad'' and ``oil is good''. I discovered an airplane recently where nose strut contained no air at all, but contained several inches too much oil instead. Once again, the preflight checklist calls for checking the height of the strut — which was completely normal. Fortunately, I noticed that the strut had no springiness whatsoever; trying to compress a solid column of hydraulic oil is like trying to compress cast iron.

To reiterate: you should make sure that the struts contain the right amount of air and the right amount of oil. Servicing a strut isn't very tricky; it just has to be done right.

10.6 Oscillations

Whenever a system has positive stability but not enough damping, you can expect to see oscillations.

10.6.1 Analysis of Dutch Roll

As remarked in section 9.3, the airplane has only a small amount of stability around the roll axis. You may be wondering why designers don't fix this problem by increasing the slip-roll coupling. The answer is that they are worried about Dutch roll.

Dutch roll is a messy combination of rolling, slipping, and yawing. As we shall see, this combined motion is less damped than the pure rolling, slipping, or yawing motions would be.

A moderate amount of Dutch roll never killed anybody, but it does tend to provoke nausea, especially in passengers.

The Dutch-roll oscillations typically have such a short period (a couple of seconds) that it is a challenge for the pilot to overcome them by working the controls. A spiral dive, on the other hand, develops much more slowly. Therefore if it comes down to a compromise between roll-axis stability and Dutch-roll damping, designers generally increase the damping at the expense of the stability.

To understand where Dutch roll comes from, and how to fight it, gives us an opportunity to combine and apply most of the things we have learned about equilibrium, stability, and damping.

The rolling and yawing motions associated with Dutch roll are shown in figure 10.6; we will discuss the slipping component in a moment.

Figure 10.6: Dutch Roll

The wingtip yaws forward, then rolls up, then yaws backward, then rolls downward, then repeats. The opposite wingtip does the same thing, 180 degrees out of phase. Imagine pedaling a bicycle backwards.

To analyze the damping of the Dutch roll system, we must remember that energy is force times distance; by the same token power (energy flow) is force times velocity. The component of the force in the direction of the velocity is the only thing that matters; the component in the perpendicular direction doesn't count.

We begin by using figure 10.7 to analyze the forces that affect the rolling motion. The velocity and position of the wingtip is shown in red; net changes in the lift vector are shown in blue.

At point A in the figure, the wing is going upward. That means it has less angle of attack than normal (and in particular, less angle of attack than the opposite wingtip). The reduced lift corresponds to a net force opposite to the velocity, and therefore energy is being removed from the system. At point C, a similar analysis applies. The wingtip is descending, creating more angle of attack and more lift than normal. This corresponds to a net force which is once again opposite to the velocity, removing energy from the system. This is the same roll damping mechanism as discussed in section 5.4.

Figure 10.7: Dutch Roll — Roll Forces

At point B, the wingtip has less velocity than normal, and less lift, while at point D the wingtip has more velocity and produces more lift. There is no effect on the damping, because the forces are perpendicular to the velocity.

We continue by using figure 10.8 to analyze the forces that affect the yawing motion. At point B in the figure, the vertical fin/rudder is wagging to the right. This changes the rudder angle of attack, opposing the motion. This is the same yaw damping mechanism discussed in section 8.3. Also, at this point, the port wingtip has less drag than the other, because it is moving backwards. Both of these effects take energy out of the system, providing damping. The same processes produce damping at point D also.

Figure 10.8: Dutch Roll — Yaw Forces

At point A, there is a little less induced drag on the port wingtip because it is flying at reduced angle of attack. This has no effect on the damping, because the force is perpendicular to the velocity.

Also at point A, there is a yawing force because the airplane's heading is not aligned with its direction of travel; the tail is too far to the left. This provides yaw-axis stability but does nothing for the yaw damping, because the force is perpendicular to the velocity.

The analysis of point C is analogous to point A.

If the yawing and rolling motions were the whole story, Dutch roll would be no problem. According to the analysis so far, there is lots of positive damping. The Dutch roll would quickly die out.

Unfortunately, nature is not so kind, as we discover when we take the sideways motion of the aircraft into account. Refer to figure 10.9.

Figure 10.9: Dutch Roll — Slip Causes Problems

At point B in the figure, the left wingtip is at the highest point in the cycle. The airplane is banked to the right. The wings' lift vector is inclined to the right, so there is a rightward component of lift. In fact, during the whole half-cycle from point A to point C there is at least some rightward force. Since the airplane has lots of inertia and not much damping² with respect to pure sideways motion, the rightward velocity just increases and increases during the whole half-cycle. The maximum rightward velocity is achieved near point C.

During the next half-cycle (from C via D to A) the airplane is banked to the left. The leftward force reduces the previously-acquired rightward velocity to zero, and then builds up a leftward velocity. The sideways velocity is zero at point D, and the maximum leftward velocity is achieved near point A.

Note that like any other lightly-damped oscillator (such as a pendulum, for instance a playground swing set) the maximum rightward force occurs when the plane is at is maximum leftward position.

The final ingredient is the slip-roll coupling.³ A certain amount of slip-roll coupling is highly desirable because it is a necessary part of the process that produces roll-axis stability (section 9.3).

The bad news is that the slip-roll coupling contributes a negative amount of damping to the Dutch roll mode. The rightward velocity is maximum at point C, producing a leftward-rolling moment. The force is in the same direction as the roll velocity, so it adds energy to the Dutch roll.

Analogously, the leftward velocity is maximal at point A, producing a rightward-rolling moment. This, too, is in the same direction as the roll velocity, contributing negative damping.

So slip-roll coupling presents designers with a dilemma: it increases roll-axis stability, but decreases (Dutch) roll damping.

The simplest way a designer can resolve this dilemma is to notice that roll-axis stability depends on both slip-roll coupling and the long-tail slip effect. Therefore if you have a problem with Dutch roll, decrease the slip-roll coupling and increase the long-tail slip effect, for instance by making the tail boom longer and reducing the rudder area. As a rule of thumb, you can tell just by looking at a short-coupled airplane that it will have a problem with underdamped Dutch roll.

The other (all too common) design choice is to sacrifice stability. Most airplanes wind up with very, very little roll-axis stability. Consequently spiral dives are a constant threat.

Note: the Dutch roll motion has some similarities and some differences when compared to the uncoordinated wing rocking exercise discussed in section 16.7. The latter is sometimes referred to as the Dutch roll exercise. The two patterns of motion share the concept of slipping to one side and then the other. The main difference is that the exercise calls for using the rudder to prevent any heading change, whereas true (natural) Dutch roll involves considerable yaw along with the banking and slipping.

10.6.2 How to Fight Oscillations

Since this book is intended for pilots, not designers, we should discuss how the pilot should use the controls in order to oppose obnoxious oscillations.

First, bit of simple advice: in an airplane that is susceptible to Dutch roll, be extra careful to avoid uncoordinated usage of ailerons and rudder since that would unnecessarily put energy into the Dutch roll mode.

Once Dutch roll gets started (due to turbulence, or klutzy control-usage, or whatever), it may be hard to stop. In some airplanes you may be able to improve the situation as follows: If the rudder pedals are moving because of the sideways force that the Dutch roll puts on the rudder, then you should rest your feet firmly on the pedals to prevent them from moving. This will increase the stability and (more importantly) the damping of the yaw axis.

If that doesn't suffice, you can try to fight the oscillations by direct intervention. This requires some skill and lots of attention.

You should not think about correcting the position of the wing. If you deflect the ailerons to the right at point D, the wings will return to level (point A) sooner, but you will be applying a force in the same general direction as the velocity, increasing the velocity and the energy of the Dutch roll mode.

As we have seen, the airplane has plenty of stability and not enough damping, so what we need is a force that depends on the velocity, not the position. Therefore the ailerons need to be deflected to the left when the left wing has its maximum upward velocity, near point A. You should apply the deflection before point A and remove it after point A. Similarly, you should apply right aileron (smoothly) a little before point C and neutralize them (gradually) after point C.

A similar analysis applies to rudder usage. Don't try to correct the position. Instead, you need to apply right rudder at the point where the nose is swinging to the left with the maximum velocity (point B); by the same token you need to apply left rudder when the nose is swinging to the right with the maximum velocity (point D).

The same logic applies to phugoid oscillation (section 6.1.12), and to pilot-induced pitch oscillation associated with a botched landing.⁴ When the nose is high, you should not push on the yoke to correct the nose-position; you should anticipate that the position will very soon over-correct all by itself. If the nose is high and dropping (or about to drop), you need a judicious pull on the yoke to prevent the pitch attitude from overshooting.

You should tell yourself that you are fighting the velocity, not trying to correct the position. This is because you need to increase the damping, not the stability.

1: On a retractable-gear airplane, you can lose all the oil, even the oil inside the hollow piston, more easily than on a fixed-gear airplane.
2: In a system with lots of damping and not much inertia, like a spoon in molasses, the velocity tends to be proportional to the applied force. In the other extreme (lots of inertia, little damping) we can apply Newton's second law without worrying about frictional forces — therefore the acceleration is proportional to the force and the velocity accumulates as long as the force is applied.
3: That is, a slip produces a rolling moment — by means of e.g. dihedral, sweepback, tall rudder, and/or shadow effects, as discussed in section 9.2.
4: Actually it is much easier to fight pitch oscillations by direct intervention, since they happen more slowly.

[Previous] [Contents] [Next]
[Comments or questions]