[Previous] [Contents] [Next]
[Comments or questions]

8 Yaw-Axis Torque Budget

In aircraft (unlike cars, bikes, or sailboats) you have separate control over which way it is pointing relative to which way it is going.

8.1 Overview

This chapter discusses the motion of the airplane around the yaw axis.¹ The conventional definitions of the three principal axes are shown in figure 19.9 in section 19.6.1. For a discussion of the terminology and general principles of forces and moments, you can refer to section 19.7. (The motion around the other axes is discussed in the following chapters.)

For a precise definition of terms such as yaw angle, heading, and slip angle, please refer to section 19.6.3.

It is important to keep the slip angle to a minimum, that is, to make sure the aircraft is pointing the same direction as it is going through the air. This is important for several reasons:

Efficiency: If your objective is to turn to the left, it doesn't make sense to let the maneuver begin with a big inadvertent yaw to the right. Also, all that slipping creates lots of unnecessary drag.
Comfort: Passengers really hate being sloshed from side to side. In many trainers, the pilots are seated so close to the pivot point (the center of mass) that they don't appreciate the effect yawing motion can have at other locations.
Safety: Whereas if you stall in coordinated flight the nose will just drop straight ahead, if you manage to stall in sufficiently uncoordinated flight, you will get a spin (see chapter 18) or a snap roll (see chapter 11), which is much harder to recover from.

Maintaining zero slip angle while maneuvering requires coordinated use of the ailerons and rudder, so pilots speak of ``zero slip angle'' and ``good coordination'' almost interchangeably.

This section considers, one by one, the various phenomena that affect the airplane's motion around the yaw axis. There are surprisingly many such phenomena, including the helical propwash, yaw-axis inertia, adverse yaw, P-factor, and gyroscopic precession — plus the stability and damping created by the vertical fin and rudder.

8.2 Yaw Stability

An airplane is not always pointing in the same direction as it is going. This is a new concept for most people, since for ordinary objects such as cars, bicycles and sailboats, the direction they are pointing is (more or less) always the same as the direction they are going, and certainly there is no separate control of the two directions.

As an extreme example of the new concept, take a Frisbee and draw on it the picture of an airplane. When you throw the Frisbee, the picture of the airplane will turn around and around and around. The direction it is pointing has no connection with the direction it is going.

In a sailboat or airplane, you can change the heading with the rudder. In the airplane (unlike the sailboat) the resulting sideways forces are too small to be of much use in changing the direction of motion (but see section 8.10).

To change the direction of flight of a Frisbee or airplane, the proper procedure is to put it into a bank and lift it around the turn.

Unlike a Frisbee, an airplane is not free to turn completely around the yaw axis. If the slip angle (i.e. the difference between the direction it is pointing and the direction it is going) gets to be more than a few degrees, performance is compromised. The vertical fin is designed to keep the slip angle from getting too large.

Figure 8.1 shows a situation where the airplane's heading has been disturbed out of its usual alignment with the airflow. There are lots of ways this could happen, including a gust of wind, a momentary uncoordinated deflection of the controls, or whatever.

Figure 8.1: Response to a Yaw Angle

In this situation, the relative wind is striking the vertical fin and rudder at an angle. Like any other airfoil, the fin/rudder produces lift in proportion to its angle of attack, so it will produce a force (and therefore a torque) that tends to re-align the airplane with the wind. We say that the airplane has lots of yaw-axis stability.

The colloquial name for yaw-axis stability is ``weathervaning tendency''. That is, the airplane tends to align itself with the relative wind, just as a weathervane does. Section 8.11 discusses weathervaning during taxi.

8.3 Yaw Damping

Pure yawing motions are reasonably well damped. The process is analogous to the process that produces damping of pure vertical motions and pure rolling motions (see chapter 5). When the tail is swinging to the right with an appreciable velocity, it sees a relative wind coming from ahead and to the right. The resulting angle of attack produces a leftward force that damps the rightward motion.

A leftward force in proportion to a rightward velocity is exactly what constitutes damping.

8.4 Helical Propwash

One of the very first things that people find out about when they start learning to fly is that it takes right² rudder (sometimes a lot of right rudder) to keep the airplane going straight at the beginning of the takeoff roll. The physics of the situation is portrayed³ in figure 8.2.

Figure 8.2: Helical Propwash

It would be nice if the propeller would just take the air and throw it straight backwards, but it doesn't. The propeller airfoil necessarily has some drag, so it drags the air in the direction of rotation to some extent. Therefore the slipstream follows a helical (corkscrew-like) trajectory, rotating as it flows back over the aircraft.

The next thing to notice is that on practically all aircraft, the vertical fin and rudder stick up, not down, projecting well above the centerline of the slipstream. That means the helical propwash will strike the left side of the tail, knocking it to the right, which makes the nose go to the left, which means you need right rudder to compensate.

You don't notice the effect of the helical propwash in cruise, because the aircraft designers have anticipated the situation. The vertical fin and rudder have been installed at a slight angle, so they are aligned with the actual airflow, not with the axis of the aircraft.

In a high-airspeed, low-power situation (such as a power-off descent) the built-in compensation is more than you need, so you need to apply explicit left rudder (or dial in left-rudder trim) to undo the compensation and get the tail lined up with the actual airflow.

Conversely, in a high-power, low-airspeed situation (such as initial takeoff roll, or slow flight) the helix is extra-tightly wound, so you have to apply explicit right rudder.

Helical propwash sometimes contributes to left/right asymmetry in multi-engine aircraft, as discussed in section 17.2.12.

8.5 P-Factor

The term P-factor is defined to mean ``asymmetric disk loading''. It is an extremely significant effect for helicopters. When the helicopter is in forward flight, the blade on one side has a much higher airspeed than the other. If you tried to fly the blades at constant angle of attack, the advancing blade would produce quite a bit more lift than the retreating blade.

8.5.1 Blade Speed

For airplanes, the same effect can occur, although it is usually small. For the effect to occur at all, you need to have an angle between the propeller axis and the relative wind. To be specific, imagine that the aircraft is in a nose-high attitude, but its direction of motion is horizontal (i.e. the relative wind is horizontal). Then the downgoing blade will be going down and a little bit forward, while the upgoing blade will be going up and a little bit backward. The downgoing blade will effectively have a slightly higher airspeed. Since this blade is on the right-hand side of the airplane (once again assuming a typical American engine) it will tend to torque the airplane around to the left and you'll need right rudder to compensate.

Figure 8.3: P-Factor

The situation is depicted in figure 8.3. The airplane is in level flight, with a 10 degree nose-up attitude. The motion of the blade through the air is shown in magenta. It consists of the rotational motion (shown in green) plus the forward motion of the whole airplane (shown in red). The motion of the downgoing blade is shown with solid lines, while the motion of the upgoing blade is shown with dotted lines. You can see that the speed of the downgoing blade is larger than the speed of the upgoing blade.

This is the main contribution to P-factor: the advancing blade sees more relative wind, while the retreating blade sees less relative wind.

8.5.2 Blade Angle

There is a widespread misconception that P-factor arises because the angle of the right (downgoing) propeller blade is larger than the angle of the left (upgoing) propeller blade. Many books erroneously call attention the angle of the blade relative to the ground. The blade doesn't care about the ground; the only thing that matters is the angle of attack, i.e. the angle between the blade and its own motion through the air.

The correct analysis is shown in figure 8.4. As a point of reference, the left panel shows level pitch attitude in normal level flight, where no P-factor occurs. Meanwhile, the right panel shows the airplane in a 10 degree nose-up attitude (still in level flight). Since we want to discuss angle of attack, I have attached a ``reference line'' pointer to each of the blades, just like the reference line used in section 2.2. The angle of attack of the propeller blade is just the angle between the reference line and the blade's motion through the air.⁴

Figure 8.4: P-Factor and Angle of Attack

When the propeller disk is inclined to the direction of flight (so that P-factor really is occurring) the downgoing blade has a slightly greater angle of attack (compared to the upgoing blade) as shown in figure 8.4. This occurs because the vector representing the airplane's motion has ``better leverage'' when it meets the resultant, because the resultant is shorter and because it is more nearly perpendicular to the airplane's motion.

This angle-of-attack effect is of course zero when propeller axis is aligned with the direction of flight.⁵ The effect is never very large, because

At low speeds, the airplane's forward velocity (as represented by the horizontal red arrow in figure 8.4 is so small that it can't have much effect on anything.
At high speeds, the airplane has a low angle of attack, so the angle between the propeller disk and relative wind is necessarily small (except for helicopters, tilt-rotors, and such).
At very high speeds, when you are going fast enough to over-run the geometric pitch of the propeller (so that the resultant coincides with the reference line in figure 8.4), you might think that a small difference in angle of attack would be a 100% effect. I suppose that's true, but in this case the total thrust is practically zero, and 100% of nothing is nothing.

This angle-of-attack effect is in addition to (and usually smaller than) the airspeed effect discussed previously. Both are small compared to the helical propwash effect.

Remember, we don't care whether the downgoing blade makes a bigger angle to the vertical than does the upgoing blade. The blade doesn't care which way is up — all it cares about is where the relative wind is coming from. Imagine a tailwheel-type airplane stationary in the run-up area on a windless day. You can incline the propeller disk as much as you want relative to vertical, but there will be no P-factor unless there is wind blowing through the propeller disk at an angle.

8.5.3 Initial Takeoff Roll

There are quite a lot of myths surrounding P-factor. For some reason, P-factor gets blamed for the fact that typical aircraft require right rudder on initial takeoff roll. This is impossible for several reasons.

Nearly everybody these days learns to fly in nose-wheel type aircraft, which means the propeller disk is vertical during the initial the takeoff roll. Since there is no angle between the relative wind and the propeller axis, P-factor obviously cannot occur.
Now let's suppose, just for sake of argument, that you are flying a taildragger, in which the propeller disk is actually non-vertical during the initial takeoff roll. Common experience is that the most right rudder is required at the very beginning of the takeoff, before much forward speed has been achieved. The Flight Training Handbook says this is because P-factor is worst at low airspeeds. But wait a minute — real P-factor is proportional to airspeed. In the initial moments of the takeoff roll, there is no relative wind, so there can't possibly be any P-factor. Of course, if you are taking off into a headwind, there could be a little bit of P-factor — but does that mean if you take off with a slight tailwind there will be a negative amount of P-factor, requiring left rudder? Don't bet on it.

The real reason that you need right rudder on initial takeoff roll is because of the helical propwash, as discussed in section 8.4. P-factor exists in some circumstances, but it cannot possibly explain the behavior we observe during initial takeoff roll.

8.5.4 Observing P-Factor

It is not easy to observe P-factor. It is hard to separate P-factor from other yaw contributions such as helical propwash (section 8.4) and twisted lift (section 8.8.4).

An important preliminary experiment is to observe what happens during the takeoff roll in a multi-engine aircraft. (To be specific, let's consider the case where the engines rotate clockwise as seen from the rear.) In some airplanes, the propwash hits the tail, and you must apply right rudder to compensate, just like in single-engine planes.

In other airplanes, most of the helical propwash misses the vertical tail in normal flight. This causes no problems and no compensation is required. See section 17.2.12 for details on this. This is the perfect way to illustrate that there is no P-factor when the propeller disk is not inclined.

If you really want to observe nonzero P-factor, you can proceed as follows: Take a twin-engine (or four-engine) aircraft with non-counter-rotating propellers. Attach a slip string. Establish coordinated cruising flight, with the same amount of power on both sides. Confirm that the ball and string are centered. Pull up into a nonturning climb at very low airspeed (i.e. very high angle of attack), maintaining cruise power. Maintain coordinated flight as indicated by the slip string. Observe the rolling tendency due to propeller drag. Shift weight (e.g. fuel) from left to right to get rid of the rolling tendency, so you can fly straight without deflecting the ailerons, i.e. without incurring any twisted lift.

You will observe the inclinometer ball will be slightly off-center. This can be attributed to P-factor. To be explicit:

Each engine is producing the same amount of thrust.
But the result is asymmetric thrust, because the location of the thrust vectors is shifted (because of asymmetric disk loading).
We have gone to some trouble to minimize other contributions, such as twisted lift. Also note that even if there were some helical propwash hitting the tail, that wouldn't be a good explanation for the off-center inclinometer. You should be able to compensate for helical propwash using the rudder alone, without banking.
To summarize: we have symmetric power settings but asymmetric thrust. A detailed analysis of the effects of asymmetric thrust can be found in section 17.2.5.

The effect of P-factor is not very large. You can easily compensate using a little bit of right rudder and right bank. Indeed, in typical situations you can just ignore it entirely.

You can never use rudder deflection as an indication of P-factor, because any situation that exhibits P-factor will also exhibit a large amount of helical propwash.

The single-engine version of the previous experiment goes like this: Put a slip string on each wing, far enough out on the wing that it is not unduly disturbed by the propwash, yet close enough in that you can see it. In a high-wing aircraft, you'll have to put the string on the bottom of the wing. Put strings on both sides in symmetric locations, so you can tell for sure what string position corresponds to symmetric airflow. Then confirm that in normal nonturning cruising flight, you have symmetric airflow (as indicated by the strings) and zero inclination (as indicated by the inclinometer ball). Finally, set up a situation in which the largest possible P-factor occurs: flaps retracted, minimum airspeed, and full power.

Once again, the indication of P-factor in this situation would be to have the ball be off-center when the strings were centered. I have tried this experiment, but the P-factor was too small to observe.

Here's another possible experiment. Take your favorite aerobatic airplane and paint the starboard rudder pedal green and the port rudder pedal red, just so we can keep straight which is which. Now go to a safe altitude and set up for inverted slow flight. In this high-power, low-speed situation, do you need to push the port (red) pedal or the starboard (green) pedal? If P-factor is more important, the answer will be port, because that is now the downgoing, advancing blade. If helical propwash is more important, the answer is starboard, because the relationship between the propeller, rudder, and rudder pedals is unchanged by the inversion.

8.6 Gyroscopic Precession

A spinning object will respond to a torque around one axis with a motion around another axis. This remarkable and counterintuitive phenomenon — gyroscopic precession — is discussed in more detail in section section 19.9.

Gyroscopic precession is often quite noticeable at the point where a taildragger raises the tail, early in the takeoff roll.⁶ If the airplane were an ordinary non-spinning object, you could raise the tail using the flippers alone. The flippers do not actually dictate the motion of the fuselage; they just produce a force and a torque around the pitch axis. For a gyroscope, a torque around the pitch axis produces a motion around the yaw axis. If you try to raise the tail of a real airplane using flippers alone, it will yaw to the left because of precession.

To get a gyroscope to actually start moving around the pitch axis, you need to apply a torque around the yaw axis. This is what the vertical fin and rudder are for. See section 19.9.

Of course, an airplane has some plain old mass in addition to its gyroscopic properties. In order to lift this ordinary mass you need to use the flippers. Therefore, the tail-raising maneuver requires both flippers and rudder — flippers to change the pitch of the ordinary mass, and rudder to change the pitch of the gyroscope.

8.7 Canted Engine

Often the engine is mounted in such a way that direction of the thrust vector is a little to one side of the axis of the airplane. This is done in order to compensate for various nonidealities such as helical propwash. It contributes to the yaw-axis torque budget in the obvious way.

8.8 Rudder Usage During Rolls

Turning the airplane properly requires coordinated use of ailerons and rudder. Getting it exactly right is a bit tricky.

Remember that in an airplane, the direction you are moving is not necessarily the same as the direction you are pointing. There are several crucial things that happen during a turn:

1): You use the wings to change the direction your center of mass is going. I call this the CM-turn.
2a): You use the rudder to change your heading (i.e. to overcome yaw-axis inertia, i.e. to provide yaw-axis acceleration).
2b): You use the rudder to overcome steady adverse yaw due to twisted lift, as discussed below.
2c): You use the rudder to overcome transitory adverse yaw due to differential drag.

Item 1 is relatively straightforward: you put the airplane into a bank. The horizontal component of lift will change the direction of motion.

Item 2a is important because if the airplane didn't have any vertical tail, banking would cause it to just slip off in the new direction without changing its heading. It is much nicer to yaw the plane to align its axis with the new direction of motion, so you apply the rudder, thereby creating a yaw rate that matches the CM-turn rate.⁷

Now we come to item 2b. We must consider adverse yaw. As discussed in section 8.8.4, during a steady roll, the aerodynamic forces produced by the two wings are equal in magnitude, but one force vector is twisted slightly forward while the other one is twisted slightly rearward. This causes a yawing moment in exactly the wrong direction: if you are rolling to the right it tries to make the airplane yaw to the left. To compensate you must deflect the rudder whenever the ailerons are deflected.

Finally, we come to item 2c. Suppose you are flying an airplane where there is a lot of mass out on the wings. Whenever you are starting or ending a roll maneuver, you need to accelerate one wing upward and the other wing downward. As discussed in section 8.8.3, this briefly requires extra lift on one wing and reduced lift on the other wing. This unequal lift produces unequal induced drag. This drag causes additional adverse yaw.

For any given rate of roll, you need to use lots more rudder at low airspeeds, for reasons discussed in section 8.8.6.

Procedures for maintaining coordination during turns are summarized in section 8.8.7; the intervening sections describe in a little more detail what is the problem we are trying to solve.

8.8.1 Analysis of a Roll

To make the discussion more concrete, let's consider a roll starting from straight-and-level flight and rolling to the right. As we can see from figure 8.5, there are multiple timescales in the problem.

Figure 8.5: Timeline for Roll Maneuver

[t0, t1] the time it takes you to move the ailerons;
[t1, t2] the time it takes for the roll rate to reach the value commanded by this aileron deflection;
[t2, t3] the time it takes the yaw rate to reach the value corresponding to the rate of CM-turn;
[t3, t4] the time you hold the ailerons deflected.

Let's analyze what happens if you move the ailerons fairly abruptly. Although generally I recommend flying with a smooth, gentle touch, (1) there will be times when you want to roll the airplane on short notice, so let's learn how to do it; and (2) the abrupt case makes it easier to understand what is going on.⁸

In some airplanes, such as a Piper Cub, the roll rate will reach its final very quickly (within a small fraction of a second), because the airplane has very little inertia about the roll axis. Practically all the mass (pilot, passenger, fuel, and engine) is arranged in a straight line right on top of the roll axis, so they don't contribute much moment of inertia. In other airplanes, such as a Cessna 310, the roll rate responds much more slowly, because lots of mass (engines and tip tanks) is situated far from the roll axis.

Before the roll rate is established (i.e. during the time [t1, t2]) the plane will experience transitory adverse yaw due to differential induced drag. The nose will swing a little toward the outside of the turn. The effect is usually rather small, since

these differential drag forces are typically small (during slow flight) or very, very small (during cruise), compared to the differential lift forces that cause the roll, and
these forces must act against the yaw-axis inertia, which is at least as large as the roll-axis inertia.

The rest of the discussion applies no matter how slowly or abruptly you moved the ailerons.

After the time t2, a steady roll rate exists. Even though the ailerons are deflected, there is no difference in lift from one wing to the other, for reasons discussed in section 8.8.4. Since there is no difference in lift, there will be no difference in induced drag, hence no transitory adverse yaw.

However, one wingtip is diving, so its force vector is twisted slightly forward. The other wingtip is rising, so its force vector is twisted slightly rearward. Even though each force has practically the same magnitude as it would in non-rolling flight, the twist means there is a slight component of force in just the right direction to produce a steady adverse yawing moment.

In addition, because the airplane has been rolling for a while, a bank has developed. This bank causes a CM-turn. The airplane is changing its direction of motion. In order to keep it pointing in the same direction it is moving, you need to use the rudder, as discussed in section 8.8.5.

At time t6, the ailerons are neutralized, but the rolling motion has not yet stopped. (Again, there is a delay due to roll-axis inertia.) At this point there are several things going on:

There is a difference in lift between the two wings, as needed to damp out the roll. This creates a negative amount of transitory adverse yaw. This requires a left-rudder contribution to compensate.
However, the airplane is still rolling, and a still-increasing rate of yaw is needed to coordinate with the still-increasing rate of CM-turn. This requires a right-rudder contribution.
Similarly, because the airplane is still rolling, the twisted lift requires a right rudder contribution.

In practical situations, the first item (transitory adverse yaw) is usually smaller than the other two.

Analogous statements would apply if you started from a left turn and used right aileron and right rudder to roll out of the turn. Similarly, it is easy to do a similar analysis for rolling into a left turn and/or rolling out of a right turn.

8.8.2 Designers' Tricks

Imagine an airplane without a vertical fin. It would behave be more like a Frisbee than a sailboat — if you gave it a yaw rate, inertia would make it just keep on yawing until some torque acted to stop it. Even if it wasn't yawing, there would be no reason to expect the yaw angle (i.e. heading) to be anywhere close to the desired value.

In a real airplane, of course, the vertical fin and rudder supply the forces required to keep the yaw angle and yaw rate under control. An overview of how you use the rudder during turns can be found in section 8.8.

Aircraft manufacturers know about how turns are affected by twisted lift and yaw-axis inertia. They generally try to provide the needed yaw-axis torque automatically, using various tricks. One trick is to interconnect the rudder and ailerons with a spring. That means you automatically get a certain amount of rudder deflection in proportion to the aileron deflection. They choose the proportionality factor so that you can more or less fly ``with your feet on the floor'' at cruise airspeeds. Of course, vastly more rudder is needed at lower airspeeds; fortunately you can easily overpower the interconnect spring by pushing on the controls in the obvious way.

Here's another trick, which you may have noticed on many airplanes: when one aileron goes down a little, the other one goes up a lot. (This is called differential aileron deflection.) The designers were trying to arrange for the upward-deflected aileron to generate a lot of parasite drag. If they do it just right, the drag force is just enough to overcome twisted lift and yaw-axis inertia during a steady roll. The so-called Frise aileron uses a similar trick. It has lip on the bottom, well ahead of the hinge. The lip sticks down into the airstream when the main part of the aileron is deflected up. Again, the purpose of the lip is to generate drag on the wing with the upward-deflected aileron.

In addition to overcoming yaw-axis inertia (during a steady roll), the designers also want to overcome transitory adverse yaw (when ailerons have been deflected but the roll hasn't yet started). Fortunately, transitory adverse yaw is rather small, and by adjusting the amount of differential deflection, and the amount of the Frise effect, pretty good cancellation can be achieved.

The bad news is that this compensation only works at one airspeed. The designers arrange it so you can fly with your feet on the floor during cruise. This is a mixed blessing, because it can lull you into complacency. At lower airspeeds, where it is most important, you still need to use lots of rudder to keep things coordinated. Don't forget!

8.8.3 Transitory Adverse Yaw

Suppose you wish to roll into a right turn. You will deflect the ailerons to the right, as shown in figure 8.6. During the brief time after the ailerons are deflected and before the steady roll is established, this will increase the lift created by the left wing, and decrease the lift created by the right wing. Unfortunately, there is no way to produce lift without producing drag, so the left wing will be dragged backwards while the right wing lunges forward. This is the exact opposite of what we wanted; the airplane yaws to the left even though we wanted it to turn to the right. Being a good pilot, you have anticipated this, so you apply right rudder as well as right aileron, to make sure the nose swings the right way.

Figure 8.6: Transitory Adverse Yaw

Even if you don't get the footwork exactly right, the nose will eventually swing around and point more-or-less the right way, because of the airplane's inherent yaw stability (as discussed in section 8.2).

Once a steady roll rate is established (no acceleration around the roll axis), the two wings are producing the same amount of lift, so this type of adverse yaw will no longer exist.⁹

Now let's consider what happens if you wish to roll out of the turn. The airplane is banked to the right and already turning to the right. You will deflect the ailerons to the left. This will cause extra drag on the right wing, and reduced drag on the left wing. The airplane will yaw to the right, continuing and exaggerating the turn that you were trying to stop. Anticipating this, you apply left rudder along with the left aileron

8.8.4 Steady Adverse Yaw -- Twisted Lift

Now let's consider what happens during a steady turn. As illustrated in figure 8.7, the airplane as a whole is moving forward, but the left wingtip is moving forward and up while the right wingtip is moving forward and down (because of the rolling motion).

Figure 8.7: Steady Adverse Yaw -- Twisted Lift

Let's see what the local angle of attack is at the wingtip. We use the trusty formula

angle of attack + angle of climb = pitch + incidence (8.1)

In the figure, the right wingtip has a negative angle of climb, since it is going forward and down. But the deflected aileron gives it a lower incidence, effectively twisting that section of airfoil nose-down. By the same token, the left wingtip has a positive angle of climb (due to the rolling motion) and an increased incidence (due to the aileron).

In a steady roll, the incidences just cancel the climb angles, so that the left wing and the right wing end up flying at the same angle of attack. If they didn't cancel, you wouldn't have a steady roll.

The cancellation means there is no torque around the roll axis, but the yaw axis is a different story. As you can see in the figure, the force vector for the downgoing wing is twisted forward, while the force vector for the upgoing wing is twisted rearward. This pair of fore-and-aft force components creates a torque around the yaw axis. You need to deflect the rudder to compensate.

Some people try to argue that these force-components should be called ``drag'' forces since they are directed fore and aft, in the same direction as the overall relative wind. However, it is much better to think of them as components of the local lift, since the twisted lift remains perpendicular to the local relative wind. The strongest argument is this: a drag force should dissipate energy in proportion to force times airspeed, but it is clear that the twisted lift forces do not dissipate energy.¹⁰

8.8.5 Yaw-Axis Inertia

(In this section, we will assume that you are flying at such a low airspeed that the designers' tricks discussed in section 8.8.2 are not sufficient to produce automatically coordinated turns.)

Whenever the airplane is in a bank, it will make a CM-turn. A pure CM-turn, however, is not what you want. A pure CM-turn means that even though the airplane is moving in a new direction, the heading hasn't changed. The airplane has a nonzero slip angle. The uncoordinated airflow acting on the tail will eventually set up a yawing motion that matches the CM-turn rate, converting it from a pure CM-turn to a more-or-less¹¹ coordinated turn. If the yaw axis damping is weak, as it usually is, the nose will slosh back and forth several times as it tries to catch up with the CM-turn.

At any particular CM-turn rate, once the yaw rate is established, no further yaw-axis torque is required. Like a toy top, once the airplane starts rotating around the yaw axis it will be happy to continue rotating.¹² The only time you need a yaw-axis torque is when the yaw rate is changing.

So, we see that during a steady roll,

The ailerons are deflected.
The bank angle is increasing and, correspondingly, the rate of CM-turn is increasing.
To match the CM-turn rate, the yaw rate must increase.
To increase the yaw rate, the rudder should be deflected.

Conclusion: the rudder should be deflected when the ailerons are deflected.

8.8.6 Amount of Rudder Required

As we have seen, there are three reasons you need to apply the rudder during roll maneuvers: yaw-axis inertia, differential induced drag, and twisted lift.

The amount of rudder deflection you need depends on the shape of your airplane, and also depends on airspeed.

* Twisted Lift

Example 1: Consider an airplane with long wings and with most of the mass concentrated near the middle of the airplane. A typical glider is an excellent example, but almost any ordinary-shaped airplane will do. In this case there will be very little roll-axis inertia, and accordingly very little transitory adverse yaw. There will also be rather little yaw-axis inertia. Therefore in such a plane, the dominant effect will be steady adverse yaw due to twisted lift.

Example 2: Suppose you are flying along in any airplane on a sunny summer day. You encounter a situation where your right wing is in an updraft, while your left wing is in a downdraft. You deflect the ailerons in order to maintain zero bank, zero roll rate, and constant heading. This combination of non-horizontal relative wind and deflected ailerons creates twisted lift, the same as shown in figure 8.7 (except that the roll rate is zero in this case). Therefore this is a perfect example of steady adverse yaw, and you must deflect the rudder to compensate. (This rudder requirement could not be explained by differential drag or yaw axis inertia. This is pure twisted lift.)

The yawing moment due to twisted lift is essentially independent of airspeed. It just depends on the deflection-angle of the ailerons. Meanwhile, though, the force produced by the rudder is proportional to airspeed squared. Therefore you need lots more rudder deflection (per unit aileron deflection) when the airspeed is low.

* Differential Induced Drag

Example 3: Consider an aircraft where there is a lot of mass located far away from the roll axis. A twin with heavy engines mounted way out on the wings, plus tip-tanks full of fuel, is a good example. Such a plane will have lots of roll-axis inertia, and therefore lots of transitory adverse yaw. You will still have to worry about yaw-axis inertia and twisted lift, but in addition to those effects you will need to apply extra rudder deflection when ailerons are first deflected, before the steady roll develops.

The amount of rudder required depends dramatically on airspeed. In addition to the rudder-force issue discussed above, the amount of transitory yawing moment itself increases when the airspeed decreases. The key to understanding this is to realize that whereas the coefficient of lift is more or less proportional to the angle of attack (for moderate angles of attack), the coefficient of induced drag is more or less proportional to the square of the angle of attack.

The left side of figure 8.8 shows the same situation as in figure 8.6, along with the coefficient of drag curve. On this curve I have indicated the different angles of attack for the two wingtips, and the correspondingly different amounts of drag. We see that the coefficient of drag curve is relatively flat on the bottom, so at relatively small angles of attack (high airspeeds), a difference in angle of attack doesn't cause too much difference in drag.

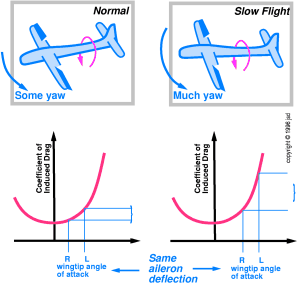Figure 8.8: Slow Flight Means More Transitory Adverse Yaw

In contrast, the right side of figure 8.8 shows the same aircraft in slow flight. Both wings are operating at a higher angle of attack. Because the coefficient of drag curve is steeper in this regime, the same difference in angle of attack (i.e. the same aileron deflection) creates more difference in drag (i.e. more transitory adverse yaw).

* Yaw-Axis Inertia

Example 4: Consider a long, thin, single-engine biplane carrying lots of cargo. Since it has a rather short wingspan, there will be rather little twisted lift, i.e. rather little steady adverse yaw. Similarly, since all the mass is close to the roll axis, there will be very little roll-axis inertia, i.e. very little transitory adverse yaw. There will, however, be lots of yaw-axis inertia.

Example 5: Let's return to the case where your right wing is in an updraft, while your left wing is in a downdraft. This time, however, you don't deflect the ailerons; you just accept the resulting roll rate. During the steady roll, you will need to deflect the rudder to supply the yaw-axis momentum to match the ever-increasing CM-turn rate. (This rudder requirement could not be explained by twisted lift or differential drag. This is pure yaw-axis inertia. Also note that no designers' tricks could maintain coordination in this situation, since the ailerons are not deflected.)

Once again, the amount of rudder required increases markedly at low airspeeds. There are three main contributions; the first two essentially cancel each other:

The roll rate depends on the deflection-angle of the ailerons, times airspeed. That means at low airspeeds the roll rate is less, which reduces the amount of rudder required.
The amount of turn that results from a given bank angle increases at low airspeeds, as discussed in section 16.6. This increases the amount of rudder required.
Finally, as always, rudder effectiveness depends on airspeed squared, increasing the amount of rudder deflection required at low airspeeds.

8.8.7 Summary: Coordinated Turning Procedures

A proper turn consist of two ingredients: a CM-turn and a heading change. In an idealized ``basic'' airplane, you would use the ailerons to bank the airplane and lift the CM around the corner, and you would use the rudder to change the heading and combat adverse yaw. In a typical modern airplane at cruise airspeeds, deflecting the ailerons alone creates a fair approximation of the proper torques around both axes. In all airplanes at low airspeeds, proper rudder usage is vitally important.

The basic rule is simple:

if you are rolling to the right, you must apply right rudder;
if you are rolling to the left, you must apply left rudder.

The amount of rudder will depend inversely on the airspeed.

Another version of the rule substitutes the word ``aileron'' for ``roll'':

right aileron requires right rudder;
left aileron requires left rudder;

In a steady roll, the two versions are more or less equivalent; at the beginning and end of a roll (when the roll rate does not match the aileron deflection) the truth lies somewhere in between. Split the difference.

The foregoing rule allows you to anticipate the need for rudder deflection. As discussed in section 11.5, you have many ways of knowing when you've got it right:

The acid test involves looking out the window. You should perceive that the rate of heading change is proportional to the amount of bank.
You can also look to the side and perceive that the wings flap straight up and down, not slicing fore and aft as you roll.
You can see that the inclinometer ball remains centered.
Yet more information comes from the seat of your pants.

By the way: If you think about it for a moment, you can see that in inverted flight (negative angle of attack) you will have a negative amount of adverse yaw — if you deflect the yoke to the left you will need to push on the right rudder pedal, and vice versa — just the opposite of what you would do in noninverted flight. When you are actually in the plane, hanging upside down, this is not as confusing as it seems on paper. A little thought and a little practice will make it fairly self-evident which wing you should lower to make a CM-turn and which rudder pedal you should push to change the heading.

As mentioned at the beginning of this chapter, there are lots of reasons why you should use the rudder properly during turns. Alas, the learning process is complicated by the fact that in many cases the airplane will ``cover up'' small mistakes for you. In particular, whenever the airplane is in a slip, the vertical fin will automatically try to return the plane to zero slip angle. This is the yaw-axis stability discussed in section 8.2. The plane will (under most conditions) eventually establish an approximately correct rate of heading change anyway. The goal of correct rudder usage is to establish the correct yaw-axis motion without a slip developing even temporarily.

The dependence of adverse yaw on airspeed can lead to trouble. Pilots spend almost all of their time buzzing around at cruise airspeeds, where ignoring the rudder is OK or nearly so. Sometimes this leads to complacency. The problem arises on approach and/or departure, where airspeeds are much lower. Proper coordination becomes more challenging, exactly at the place where it is most important (since the margins for error are also smaller). If you mishandle the ailerons at low speed and low altitude, you could well cause a spin or a snap roll, with no chance for recovery.

Section 11.5 describes a few useful tricks for perceiving exactly how much rudder is needed to achieve perfect coordination.

8.9 Long-Tail Slip

Now let's see what happens while the airplane is in an established turn. In particular, let's consider an airplane with a fairly long fuselage, flying in a fairly tight turn. As shown in figure 8.9, there is no way that the airflow can be lined up with the front part of the fuselage and the back part of the fuselage at the same time. The fuselage is straight, and the path through the air is curved. You can't have a straight line be tangent to a circle at two different points. You have to choose.

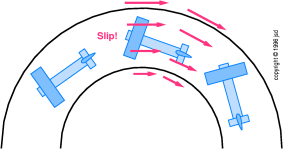Figure 8.9: Airplane in a Tight Turn — Rudder Neutral

If left to its own devices, the airplane will choose to have the vertical fin and rudder lined up with the airflow. The fin/rudder combination is, after all, an airfoil. Airfoils are good at producing tremendous forces if the wind hits them at an angle of attack. Besides, the tail is way back there where it has a lot of leverage around the yaw axis.

Because of the air hitting the sides of the fuselage, and other effects, the fin/rudder might not completely determine the slip angle, but it will be the main determining factor. For sure, the airflow at the front of the fuselage — and over the wing — will have a significant slip component.

This will occur whenever the airplane is in a turn (unless you explicitly deflect the rudder to compensate). I call this the long-tail slip effect. This slip sounds like a bad thing, but in fact it can be put to good use; without it there would be no roll-axis stability, for reasons discussed in section 9.3. Remember: an inadvertent turn will be a slipping turn.

You can see from the geometry of the situation that the amount of long-tail slip is proportional to the length of the airplane and inversely proportional to the turning radius. The latter depends on the square of the airspeed, as well as the bank angle.

In a stubby, fast aircraft like a V-tailed Bonanza in a 15 degree bank at 165 knots, the long-tail slip effect will be small fraction of a degree — hardly noticeable. On the other hand, in a long, slow glider, maneuvering to stay in a thermal using a 45 degree bank at 50 knots, the effect will be fifty or a hundred times greater! You will need several degrees of rudder deflection. You may need to push the rudder pedal all the way to the floor just to keep the air flowing straight over the wings. (Even if you decide to accept a little slip over the wings in order to reduce the crossflow over the fuselage and stabilizer, you will still want inside rudder, and lots of it.)

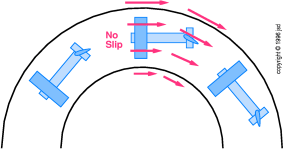Figure 8.10: Airplane in a Tight Turn — Rudder Deflected

I emphasize that even though you are holding inside rudder (bottom rudder) during the turn, this is definitely not a skidding turn (unless you get carried away and use too much inside rudder). This rudder usage is completely unrelated to the uncoordinated ``boat turn'' discussed in section 8.10.

We would like the airflow to be aligned perpendicular to the wings and parallel to the fuselage everywhere, but in a tight turn this is not possible. We have to compromise and ``split the difference''. The lowest-drag arrangement is to have at the nose a slight crossflow from inside the turn, and at the tail a slight crossflow from outside the turn.

The best way to check the alignment is with a slip string¹³ — a piece of yarn exposed to the airflow where the pilot can see it. If (as is usually the case) you don't have a slip string, you can refer to the inclinometer ball.¹⁴

8.10 Boat Turn

My friend Larry has a sailboat. It doesn't have ailerons. You steer it with the rudder.¹⁵ This changes the direction the boat is pointing. As shown in figure 8.11, this causes the water to flow crosswise past the hull, creating a sideways force that eventually changes the direction the boat is going.

Figure 8.11: Boat Making a Boat Turn

Figure 8.12: Airplane Making a Boat Turn

All the same words can be applied to an airplane. Keeping the wings level, you press the right rudder pedal. This causes the airplane to yaw to starboard. As shown in figure 8.12, air will then hit the fuselage on the port side, creating a sideways force¹⁶ that will gradually shove the airplane around in a right-hand turn. (There will also be a lot of drag, but that is not our concern at the moment.) The force of the wind on the rudder (needed to yaw the plane) is smaller than, and in the opposite direction to, the resulting force of the wind on the fuselage.

In powered flight, the horizontal component of thrust will make an additional contribution to the boat turn.

To reiterate: the airplane will turn to the right if you hold the right rudder pedal down — even if the wings are not banked. Of course, turning the airplane properly (using the wings) is ten times more effective and more efficient than a boat turn

8.11 Weathervaning During Taxi

When the airplane is on the ground, it feels the force of the ground and the force of the wind.

Since the tail is far, far behind the wheels, a crosswind will create a torque around the yaw axis. It will tend to blow the tail downwind, forcing the nose to turn upwind, just like a weathervane.

Now, suppose you are moving (as opposed to parked). The weathervaning tendency causes the nose to turn into the wind. The wheels are still on the ground, making lots of friction, so the airplane will roll in the direction determined by the wheels, i.e. the direction it is heading. Therefore the airplane will travel toward the upwind side of the runway. This may seem ironic or even paradoxical, but it's true — the crosswind causes the airplane to move upwind.¹⁷ You have to deflect the rudder to downwind to compensate.

8.12 Asymmetric Thrust

In a multi-engine airplane, if the engine on one side has failed, or for any reason is developing less thrust than its counterpart on the other side, this will produce a torque (possibly a very large torque) around the yaw axis. This is discussed in section 17.2.4.

8.13 Yaw-Axis Torque Budget — Summary

We have finally come to the end of this section, having covered the most important causes and effects of torques and motions around the yaw axis. There are quite a number of such processes:

The helical propwash effect is important, especially in high-power / low-airspeed situations.
Gyroscopic precession means that deflecting the flippers will cause a yawing motion (and deflecting the rudder will cause a pitching motion).
Adverse yaw means that deflecting the ailerons will cause a yawing moment.
The long-tail slip effect means that an inadvertent turn will be a slipping turn. This effect is very significant in gliders. It is much less noticeable in typical powered aircraft, but it has important implications for roll stability, as discussed in section 9.3.
P-factor exists in principle but is usually insignificant.
Actual motion around the yaw axis will create a yawing moment that tends to damp the motion.
Yawing the plane changes the direction it is pointing which does not automatically change the direction it is going; the ``boat turn'' effect exists but is feeble and inefficient.
The pilot can deflect the rudder to oppose the unwanted yawing effects and create the desired ones.

Some of these ideas will be revisited when we discuss ``Dutch roll'' in section 10.6.1.

Perceiving coordination and maintaining coordinated flight is important. Further discussion of this topic appears in chapter 11, along with a discussion of how and why to perform intentional slips.

1: For a discussion of the terminology of forces and moments, you can refer to section 19.7.
2: All the examples in this section assume a typical American engine that rotates clockwise as seen from behind.
3: The figure exaggerates the curvature of the streamlines.
4: You can also think of the blade's angle of attack as the angle between the reference and the blade's relative wind. Relative wind and direction of motion are the same concept, just reversed 180 degrees. Be careful though, because there are various different relative winds, including the instantaneous wind relative to the moving blade and the average wind relative to the overall airplane.
5: Interestingly, it goes to zero again when the axis is perpendicular to the direction of flight, as in a helicopter.
6: but if you pay attention you can notice it in many other situations
7: Yaw-axis acceleration (which may be a somewhat unfamiliar subject) is discussed in more detail in section 8.8.1.
8: This analysis ignores the overbanking tendency and various other small effects.
9: Although in a steady turn you may need some rudder deflection because of the long-tail slip effect, as discussed in section 8.9, and in a steady roll you will need some rudder deflection because of twisted lift and roll-axis inertia, as discussed in the following sections.
10: The real drag vector gets twisted, too, but the consequences are too small to worry about.
11: It won't be exactly coordinated because of the long-tail slip effect, as discussed in section 8.9.
12: But you will generally need some rudder deflection to compensate for the long-tail slip effect.
13: This is more commonly called a yaw string, but in fact it measures the slip angle, not the yaw angle. This is discussed in more detail in section 17.2.3.
14: However, the inclinometer ball and the slip string actually measure quite different things. The difference is important if you have asymmetric thrust, as discussed in section 17.2.4.
15: Boat lovers' note: there are some ocean liners that do use roll-control devices rather like ailerons, although they are primarily for passengers' comfort, not for steering. Also, to be sure, there are some boats that can be steered by banking them. On my sailboard, for instance, you have to bank it the wrong way (i.e. to the outside of the turn) by shifting your weight. On some light racing yachts you can steer them pretty well just by shifting the weight of the crew around. Many speedboats bank into the turns. But we're getting off the subject. The point is that Larry's boat (like lots of others) leans to leeward whether you are turning left, turning right, or going straight. The reason it doesn't tilt any more than it does is because there are a couple thousand pounds of lead in the keel. You can't bank it by shifting your weight, and it wouldn't turn much if you did. You steer it with the rudder.
16: Technically, this force is classified as a lift force, since it is perpendicular to the relative wind — even though it is produced by the fuselage (not the wings), and even though it is horizontal. See the official definitions in chapter 4.
17: In those rare cases where there is inadequate friction on the wheels (such as a seaplane, or an airplane taxiing on a slick icy surface) it is quite possible for the wind to blow the airplane downwind. This of course has nothing to do with torque; it's just a plain force.

[Previous] [Contents] [Next]
[Comments or questions]